Реферативный проект по теме «Углы в пространстве»
 Скачать 260.37 Kb. Скачать 260.37 Kb.
|
                                                                                                           Министерство образования Нижегородской области Муниципальное автономное образовательное учреждение средняя общеобразовательная школа № 58 посёлок Мулино Володарский район п. Мулино Проблемно-реферативный проект по теме «Углы в пространстве» Выполнил: Гладков Дмитрий обучающийся 11класса МАОУ СОШ №58 Руководитель: Байгулова Нина Витальевна учитель математики высшей квалификационной категории МАОУ СОШ №58 2013 год ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 3 ГЛАВА I. СПРАВОЧНЫЙ МАТЕРИАЛ §1. Из истории геометрии 5 §2.Полезно знать 6 ГЛАВА II. СПОСОБЫ НАХОЖДЕНИЯ УГЛОВ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ §3. Параллельный перенос 7 3.1 Куб 7 3.2.Шестигранная призма 8§4. Метод координат 9 4.1. Координаты куба 10 4.2. Координаты трехгранной призмы 11 4.3. Координаты шестигранной призмы 12 4.4. Координаты четырехугольной пирамиды 14§5. Способ «в три косинуса» 16 §6. Правило тетраэдра 17 ГЛАВА III. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ: «ЗАДАНИЯ С2 ЕГЭ» §7. Три способа решения одной задачи С2 18 7.1. Решение 1 (по теореме о 3 перпендикулярах) 18 7.2. Решение 2 (параллельный перенос) 18 7.3. Решение 3(метод координат) 19 §8. Решите сами 19 ЗАКЛЮЧЕНИЕ 21 ИСТОЧНИКИ МАТЕРИАЛОВ Приложения ВВЕДЕНИЕ Тема моего проекта «Углы в пространстве». С понятием угла мы встречаемся в повседневной жизни. Примером тому служит угол между электрическими проводами, т.е. прямыми (рис.1). Угол, образованный кольями и землёй - это угол между прямой и плоскостью (рис. 2). Крылья бабочки составляют угол – это угол между плоскостями (рис. 3).   Рис. 3  Рис. 2 Рис.1
В самой природе очень много замечательных геометрических форм. Она сама, без вмешательства человеческих рук создаёт геометрию красоты, гармонии. В земле иногда находят камни такой формы, как будто их кто-то тщательно выпиливал, шлифовал, полировал. Это многогранники с плоскими гранями и прямыми ребрами (рис. 6). Правильные и совершенные формы этих камней, безукоризненная гладкость их граней поражают нас. Трудно поверить, что такие идеальные многогранники образовались сами, без помощи человека. Кристалл соли имеет форму куба. Кристаллы горного хрусталя напоминают отточенный с двух сторон карандаш. Алмазы чаще всего встречаются в виде октаэдра, иногда куба. Существуют и многие микроскопические многоугольники. В микроскоп можно увидеть, что молекулы воды при замерзании располагаются в вершинах и центрах тетраэдров. Одна из самых изысканных геометрических фигур падает на нас с неба в виде снежинок. Но самые искусные геометры – пчёлы. Они строят соты из шестиугольников (рис. 7). Любая ячейка в сотах окружена шестью другими ячейками. А основание, или донышко, ячейки представляет собой трехгранную пирамиду. Такая форма выбрана неспроста. В правильный шестиугольник поместится больше меда, а зазоры между ячейками будут минимальными. Разумная экономия усилий и строительных материалов. Рис.6  Рис.7  Цели проекта:
Задачи проекта:
ГЛАВА I. СПРАВОЧНЫЙ МАТЕРИАЛ «Жизнь не спросит, что ты учил. Жизнь спросит, что ты знаешь» §1. Из истории геометрии Геометрия зародилась в Древнем Египте 5-6 тысяч лет назад, как набор правил решения практических задач, возникших в строительстве при распределении земельных участков, измерении площадей и объемов и т.д. Ещё в эпоху неолита люди составляли на стенах пещер орнаменты из треугольников, ромбов, прямоугольников, кругов. Древние художники тонко чувствовали красоту геометрических форм; наскальные рисунки, выполненные с большой любовью к природе, радовали глаз. Человек отмечал равенство, симметрию, подобие фигур. Со временем он научился использовать свойства фигур в практической жизни. Геометрия применялась при постройке величественных зданий: пирамиды Хеопса (рис.8), Колизея (рис. 9), Амфитеатра (рис.10), которые стоят и, по сей день. Рис. 8. Пирамида Хеопса  Рис. 9. Колизей  Рис.10. Амфитеатр  Геометрия – древнейшая наука, а первые геометры производили расчеты свыше тысячи лет назад. Земледельцы, жившие на берегах великих рек: Нила, Тигра и Евфрата, Инда и Ганга, искусно делили свои земельные участки. Для проведения замеров были выработаны первые правила новой науки – «геометрии», что в переводе с греческого и означает – «землемерие». «Начала» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии. «Начала» — вершина античной геометрии и античной математики вообще, итог её 300-летнего развития и основа для последующих исследований. «Начала», наряду с двумя трудами Автолика из Питаны — древнейшее из дошедших до нас античных математических сочинений; все труды предшественников Евклида известны нам только по упоминаниям и цитатам позднейших комментаторов. Евклидова геометрия предполагает, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении. После Евклида многие поколения математиков стремились улучшить данную им систему аксиом. Большую роль сыграли работы современника Евклида – древнегреческого учёного Архимеда, который сформулировал аксиомы, относящиеся к измерению геометрических величин. Из математиков более позднего времени большой вклад в усовершенствование аксиоматики геометрии внесли замечательный русский математик Н.И.Лобачевский, немецкий математик Д.Гильберт, венгерский математик Я.Больяй, «король математики» К.Ф.Гаусс и другие учёные. Евклид  Н. И. Лобачевский Н.И.Н.И.Лобачевский  К.Ф. Гаусс  §2. Полезно знать При нахождении угла между скрещивающимися прямыми необходимо знать:
ГЛАВА II. СПОСОБЫ НАХОЖДЕНИЯ УГЛОВ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ Решая и исследуя задания на нахождение угла между скрещивающимися прямыми, я выделил следующие 4 способа:
§3. Метод «Параллельного переноса» Многие задачи стереометрии можно решить, используя параллельный перенос прямых, то есть смещение всех точек прямой в одном и том же направлении на одно и то же расстояние. Посмотрим, как этот способ можно использовать при нахождении угла между скрещивающимися прямыми. Предлагаю разобрать несколько конкретных примеров. 3.1 Куб Задача 1. В единичном кубе АВСDА1В1С1D1 найдите угол между прямыми АВ1 и ВС1. Решение. Прямая AD1 параллельна прямой ВС1. Угол между прямыми АВ1 и ВС1 равен углу В1AD1. Так как грани куба равные квадраты, то их диагонали равны: АВ₁= AD1 = В₁D1 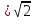 (по теореме Пифагора). Следовательно, треугольник В1AD1 – равносторонний, значитÐ В1AD1 = 600 . (по теореме Пифагора). Следовательно, треугольник В1AD1 – равносторонний, значитÐ В1AD1 = 600 .Ответ: 60. Задача 2. В кубе ABCDA₁B1C1D1 все ребра равны 1.Найдите угол между прямыми АВ и CB1. Решение. В кубе ребра АВ и CD параллельны. Угол между прямыми АВ и CВ₁ равен углу между СВ₁ и CD , то есть углу DСВ₁ . По свойству куба Ð DСВ₁ = 900. Ответ: 90. Задача 3. В кубе ABCDA₁B₁C₁D₁ все ребра равны 1.Найдите угол между прямыми АС и BD₁. С2 D2 В2 A2 Решение. Построим ещё куб BА₂В₂CB₁C₂D₂С₁ с ребром равным 1. Прямая ВВ₂ параллельна прямой АС. Угол между прямыми АС и BD₁.равен углу D₁ВВ₂ Диагональ куба BD₁= 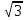 , диагональ квадрата ВВ₂= , диагональ квадрата ВВ₂=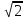 . Отрезок D₁B₂ = . Отрезок D₁B₂ =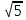 ,как диагональ прямоугольника со сторонами 1 и 2. Для треугольника D₁ВВ₂ проверим теорему Пифагора: ,как диагональ прямоугольника со сторонами 1 и 2. Для треугольника D₁ВВ₂ проверим теорему Пифагора: 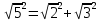 . Значит треугольник D₁ВВ₂ – прямоугольный, Ð D₁ВВ₂ = 900 . . Значит треугольник D₁ВВ₂ – прямоугольный, Ð D₁ВВ₂ = 900 .Ответ: 90. 3.2.Шестигранная призмаЗадача 4. В правильной шестиугольной призме ABCDEFAB1C1D1E1F1 все ребра равны 1.Найдите угол между прямыми АВ и A1С1. E₁ D₁ С С₁ А₁ D F₁ F В А В₁ E Решение. Построим прямую АС параллельную А₁С₁, и найдём угол САВ. Треугольник АВС – равнобедренный, Ð АВС = 1200 (по свойству правильного шестиугольника), Следовательно, Ð САВ = 300 . Ответ: 30. Задача 5 В правильной шестиугольной призме A … F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1 . 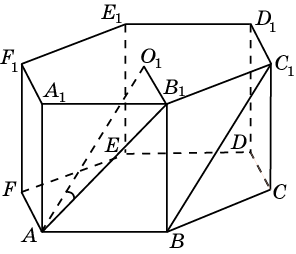 Решение. Пусть O1 – центр правильного шестиугольника A1…F1. Тогда, прямая AO1 параллельна прямой BC1, и искомый угол φ между прямыми AB1 и BC1 равен углу B1AO1. В равнобедренном треугольнике B1AO1 имеем: O1B1 = 1; AB1=AO1= 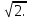 Применяя теорему косинусов, получим Применяя теорему косинусов, получим 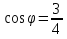 . .Ответ: 0,75. §4. Метод координат Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их ввожу сам: указав начало отсчета, единичный отрезок и направление осей x, y и z. Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Но во всех случаях упор делаю на минимизацию объема вычислений. Если все вычисления будут правильными, то и ответ будет правильным. И конечно полезно знать: - формулу вычисления длины отрезка и координат середины отрезка (см. Приложение 10); - правила нахождения координат вектора и его длины, координат суммы и разности векторов, координат вектора умноженного на число (см. Приложение11); - формулу нахождения угла между векторами (см. Приложение12). 4.1. Координаты куба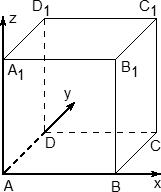 Систему координат предлагаю ввести следующим образом:
Итак, теперь у каждой вершины куба есть координаты.
Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, найдя координаты направляющих векторов a (x1; y1; z1) и b (x2; y2; z2), мы сможете найти угол. Точнее, косинус угла по формуле: cos φ = 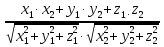 Посмотрим, как эта формула работает на конкретных примерах. Задача 1. В единичном кубе АВСDА1В1С1D1 найдите угол между прямыми АВ1 и ВС1. х у z Решение. Введем систему координат: начало в точке A, оси x, y, z направим вдоль рёбер AB, AD и AA1 соответственно. Поскольку ребро куба не указано, положим AB = 1, тогда единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых. Для этого вычислим координаты точек: А(0; 0; 0), В₁(1; 0; 1), В(1; 0; 0), С₁(1; 1; 1). Тогда координаты векторов равны: АВ₁(1; 0; 1), ВС₁(0; 0; 1). Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому cos a = 1/2, следовательноÐ (АВ1;ВС1)=600. Ответ: 60. 4.2. Координаты трехгранной призмыПроведённые мною исследования вариантов ЕГЭ показали, что в задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). 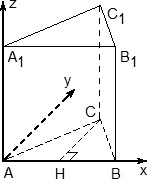 Для них систему координат ввожу почти так же, как и для куба: 1) начало координат — в точке A; 2)сторону призмы принимаю за единичный отрезок, если иное не указано в условии задачи; 3) ось Оx направляю по ребру AB, Оz — по ребру AA1, а ось Оy расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC. Сделаю некоторые пояснения. Дело в том, что ось Оy НЕ совпадает с ребром AC, так как треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:  Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C. Получаем следующие координаты точек:
Рассмотрим конкретные примеры. Задача 6. В правильной трехгранной призме ABCA1B1C1, все ребра которой равны 1, отмечены точки D и E — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AD и BE. z у х 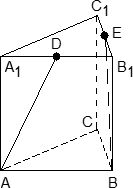 Решение. Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA1. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых. Рассмотрим точки: A (0; 0; 0) и D(0,5; 0; 1), т.к. D — середина отрезка A1B1. Поскольку начало вектора AD совпадает с началом координат, получаем AD (0,5; 0; 1). Точка B(1; 0; 0), Е( 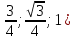 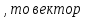 BE(- BE(-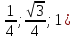 . . Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому cos φ = 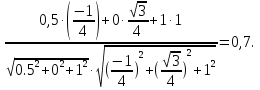 Ответ: arccos 0,7. 4.3. Координаты шестигранной призмыШестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы. 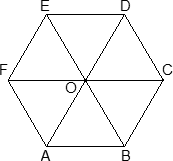 Ввести систему координат предлагаю следующим образом. Начало координат , точку O, поместим в центр симметрии шестиугольника ABCDEF. Ось Оx пойдет вдоль FC, а ось Оy — через середины отрезков AB и DE. Получим такую картинку: 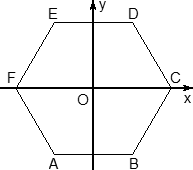 Обратите внимание: начало координат не совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений. Осталось добавить ось Оz. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. 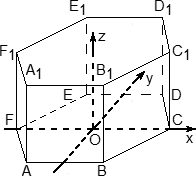 Предположим, что все ребра нашей правильной шестигранной призмы равны 1, тогда координаты вершин следующие:
Рассмотрим задачу на это правило. Задача 7. В правильной шестигранной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, отмечены точки K и L — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AK и BL. у z х 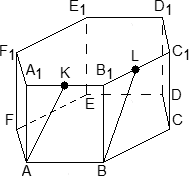 Решение. Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Точки K и L — середины отрезков A1B1 и B1C1 соответственно, поэтому их координаты находятся через среднее арифметическое. Координаты интересующих нас точек равны: A(- 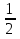 ;- ;- 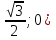 , K(0; , K(0;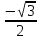 ;1), B( ;1), B(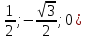 , L( , L(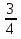 ;- ;-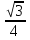 ;1) ;1)Найдем координаты направляющих векторов AK и BL: AK(0,5;0;1), BL( 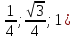 . .Теперь найдем косинус угла: cos φ = 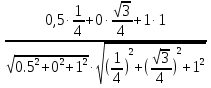 = 0,9. Ответ: arccos 0,9. = 0,9. Ответ: arccos 0,9. 4.4. Координаты четырехугольной пирамидыМы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже привожу общую схему вычисления координат. И так, правильная четырехугольная пирамида. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. 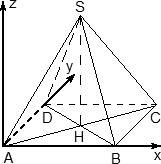 Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H (0,5; 0,5; 0).Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Посмотрим, как этот приём работает на конкретных примерах. Задача 8. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF. у z x  Решение. Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1. Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек: A(0; 0; 0); B(1; 0; 0), E( 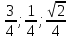 ), F( ), F(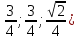 . .Зная точки, найдем координаты направляющих векторов AE и BF: AE( 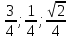 ) , BF( ) , BF(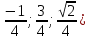 . .Найдём косинус угла между векторами по формуле: cos 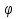 = =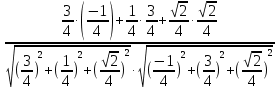 = =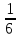 . . Ответ: arccos 1/6. Я рассмотрел лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. §5. Способ «в три косинуса» b a b1 В некоторых задачах при нахождении угла между скрещивающимися прямыми полезно воспользоваться следующим алгоритмом: 1) построить плоскость, в которой лежит прямая а, и прямая b пересекает эту плоскость; 2) построить b 1 проекцию прямой b на эту плоскость. Если прямые a и b 1 пересекаются, прямые b и b 1 пересекаются то: Cos Ðab =Cos Ðab 1 · Cos Ðbb . Посмотрим, как эта формула работает на конкретных примерах. Задача 1. В единичном кубе АВСDА1В1С1D1 найдите угол между прямыми АВ1 и ВС1. Решение. Прямая BC₁ лежит в плоскости (B₁BC). Построим проекцию ребра АВ₁ на плоскость (B₁BC) . Применяя формулу Cos ÐAB1,BC1 =Cos ÐAB1B ·Cos ÐB1BC1 , получаем Cos ÐAB1,BC1 =0.5, значит Ð(AB1,BC1)=60° . Ответ: 60. §6. Правило тетраэдра D В А С 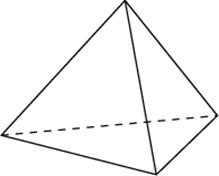 Для вычисления угла между скрещивающимися прямыми можно использовать правило тетраэдра: CosÐ (AD;BC)= 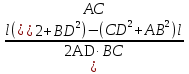 . .Посмотрим, как эта формула работает на конкретных примерах. Задача 1. В единичном кубе АВСDА1В1С1D1 найдите угол между прямыми АВ1 и ВС1. В D₁ А₁ А D C₁ B₁ С 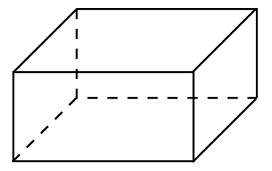 Решение. Построим тетраэдр с противоположными ребрами AB₁ и BC₁. Применяя формулу CosÐ (AВ₁;BC₁)=  , , получаем Cos ÐAB₁,BC₁ =0.5. Следовательно , Ð(AB₁,BC₁)=60° . Ответ: 60. ГЛАВА III. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ: «ЗАДАНИЯ С2 ЕГЭ» Мною исследованы и обобщены 4 способа нахождения угла между скрещивающимися прямыми: с помощью параллельного переноса; метод координат; способ в «три косинуса»; правило тетраэдра. Можно приступать, собственно, к методам решения конкретных заданий C2 ЕГЭ, среди которых много задач на нахождение угла между скрещивающимися прямыми. §7. Три способа решения одной задачи С2 Предлагаю 3 способа решения следующей задачи. Задача 9. (Слайд 41) В правильной шестиугольной призме A … F1, все ребра которой равны 1, найдите угол между прямыми AB1 и BE1. 7.1. Решение 1 (по теореме о 3 перпендикулярах) 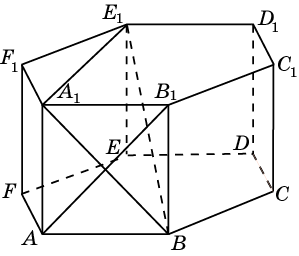 Докажем, что угол между прямыми AB1 и BE1 равен 90о. Для этого воспользуемся теоремой о трех перпендикулярах. А именно, если ортогональная проекция наклонной на плоскость перпендикулярна прямой, лежащей в этой плоскости, то и сама наклонная перпендикулярна этой прямой. Ортогональная проекция BE1 на плоскость ABB1 есть прямая A1B, перпендикулярная AB1. Следовательно, прямая BE1 также будет перпендикулярна прямой AB1, т.е. искомый угол равен 90о. Ответ: 90. 7.2. Решение 2 (с помощью параллельного переноса) 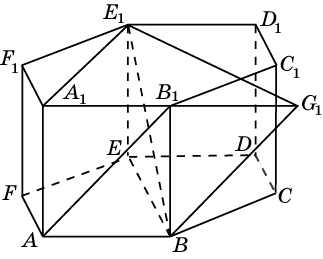 Через точку B проведем прямую, параллельную прямой AB1, и обозначим G1 ее точку пересечения с прямой A1B1. Искомый угол равен углу E1BG1. Сторона BG1 треугольника E1BG1 равна √2 . В прямоугольном треугольнике BEE1 катеты BE и EE1 равны соответственно 2 и 1. Следовательно, гипотенуза BE1 равна √5. В прямоугольном треугольнике G1A1E1 катеты A1G1 и A1E1 равны соответственно 2 и √3. Следовательно, гипотенуза G1E1 равна √7 . Таким образом, в треугольнике BE1G1 имеем: BG1 = √2 , BE1 = √5 , G1E1 =√7 . По теореме, обратной к теореме Пифагора, получим, что угол E1BG1 равен 90о. Ответ: 90. 7.3. Решение 3 (метод координат) 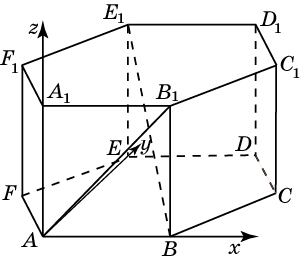 Введем систему координат, считая началом координат точку A, точка B имеет координаты (1, 0, 0), точка A1 имеет координаты (0, 0, 1), точка E имеет координаты (0, √3 , 0). Тогда точка E1 имеет координаты (0, √3 , 1), Вектор АВ₁ имеет координаты (1, 0, 1), вектор ВЕ₁ имеет координаты (-1,√3, 1). Тогда скалярное произведение векторов АВ₁ и ВЕ₁ равно 0. Значит и косинус угла между этими векторами равен 0. Следовательно, искомый угол равен 90о. Ответ: 90. §8. Решите сами Если вы хотите правильно выполнить задание С2 на ЕГЭ, нужно знать не только правила и способы решения, но важно найти рациональный метод. А здесь нужна тренировка. Поэтому предлагаю несколько задач на нахождение угла между скрещивающимися прямыми для самостоятельного решения.
Ответ: arccos 0,8.
Ответ:1/3. 3. Ребро куба равно 3. Найдите угол между прямыми AE и BF, если BE= 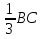 C1F= 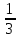 C1B1 . C1B1 .Ответ: arccos 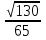 . .
Ответ: arccos 0,25. 5. В правильной шестиугольной призме все ребра равны 1. Найдите косинус угла между прямыми АВ1 и ВF1. Ответ: 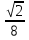 6. В правильной шестиугольной призме A … F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1. Ответ: 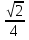 . .7. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямыми ВМ и DE, где М — середина ребра SC. Ответ: 1. 8. В правильной треугольной призме ABCA₁В₁С₁, все рёбра которой равны 1,найдите расстояние между прямыми AA₁ и BC₁. Ответ: √(3)/2. При оценивании выполнения заданий С2 нужно использовать следующие критерии:
ЗАКЛЮЧЕНИЕ Исследование мною заданий на нахождение угла между скрещивающимися прямыми показало: - угол можно найти несколькими способами; - для каждой задачи можно найти рациональный метод решения. Выполняя задания на нахождение угла между скрещивающимися прямыми, я заметил, что в большинстве задач этого типа сложность вызывают необходимые построения рисунка. В этом случае рациональнее решить задачу методом координат. Рекомендации Мой проект может быть использован на уроках математики и факультативных занятиях, как при объяснении нового материала, так и при обобщении знаний по теме «Многогранники». Работа может быть полезна учащимся при отработке навыков решения заданий C2 ЕГЭ. ИСТОЧНИКИ МАТЕРИАЛОВ
|


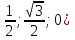
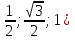
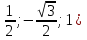
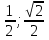 )
)