Системно-деятельностный подход в обучении математике
 Скачать 145.79 Kb. Скачать 145.79 Kb.
|
 Системно-деятельностный подход в обучении математике Системно-деятельностный подход в обучении математикеБайгулова Нина Витальевна учитель математики МАОУ СОШ №58 «Когда людей станут учить не тому, что они должны думать, а тому, как они должны думать, то тогда исчезнут всякие недоразумения» Г. Лихтенберг. Вместо простой передачи ЗУН от учителя к ученику приоритетной целью школьного образования становится развитие способности ученика самостоятельно ставить учебные цели, проектировать пути их реализации, контролировать и оценивать свои достижения, иначе говоря, умение учиться. Воспитание умения учиться понимается сейчас как ведущая ценность и цель образования XXI века. Системно-деятельностный подход в обучении и воспитании дает высокие результаты, соответствующие современным ценностям и целям образования, удачно синтезирует позитивные элементы традиционной модели обучения и имеющихся альтернативных развивающих систем обучения. Системно-деятельностный подход перспективен в качестве средства реализации новой концепции Федеральных государственных образовательных стандартов, доступен для освоения в массовой практике всеми звеньями системы образования. «Репродуктивная школа выращивает в лучшем случае информированных людей, хорошо решающих кроссворды, но беспомощных в новой ситуации, не приспособленных жить в нынешнем быстро меняющемся мире без постоянного руководства, надзора и опеки». Перемены, происходящие в современном обществе, требуют ускоренного совершенствования образовательного пространства, определения целей образования, учитывающих государственные, социальные и личностные потребности и интересы. В связи с этим приоритетным направлением становится обеспечение развивающего потенциала новых образовательных стандартов. Развитие личности в системе образования обеспечивается, прежде всего, через формирование универсальных учебных действий, которые выступают инвариантной основой образовательного и воспитательного процесса. Овладение учащимися универсальными учебными действиями создают возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, то есть умения учиться. Эта возможность обеспечивается тем, что универсальные учебные действия – это обобщенные действия, порождающие широкую ориентацию учащихся в различных предметных областях познания и мотивацию к обучению. Мне хочется рассказать о системно-деятельностном подходе в обучении математике. При этом подходе выделяются следующие компоненты овладения знаниями по математике: а) восприятие информации; б) анализ полученной информации (выявление характерных признаков, сравнение, осознание, трансформация знаний, преобразование информации); в) запоминание (создание образа); г) самооценка. При организации учебной деятельности по математике обращаю внимание на то, чтобы у учащихся сформировались потребности в осуществлении творческого преобразования учебного материала с целью овладения новыми знаниями. А для того, чтобы знания учащихся были результатом их собственных поисков, организую эти поиски, управляю учащимися, развиваю их познавательную деятельность.   Позиция учителя: к классу не с ответом (готовые знания, умения, навыки), а с вопросом. Позиция ученика: за познание мира, (в специально организованных для этого условиях). Учебная задача – задача, решая которую ребенок выполняет цели учителя. Она может совпадать с целью урока или е совпадать. Учебная деятельность – управляемый учебный процесс. Учебное действие – действие по созданию образа. Образ – слово, рисунок, схема, план. Оценочное действие – я умею! У меня получится! Эмоционально – ценностная оценка – Я считаю так то…. (формирование мировоззрения) Урок-игра Девиз урока: “Никогда не беритесь за последующее, не усвоив предыдущее”. И. Павлов Тема урока:«Все действия с обыкновенными дробями» Класс: 5 Предмет:математика Авторы учебника: С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин Номер урока в теме: 35 Тип урока: обобщение и систематизация знаний Цели:
Оборудование: - плакаты с изображением домиков, деревьев, леса, гор; - карточки к игре «Поле чудес» и к проверочной работе; - сигнальные карточки к устным упражнениям; - модели цветов; - компьютерная презентация урока. Структура урока:
Ход урока 1.Организационный момент 2.Постановка цели урока и мотивация учебной деятельности учащихся 1)Ребята, сегодня мы отправимся с вами в необычное путешествие, мы посетим страну «Обыкновенные дроби». В этой стране мы сделаем несколько остановок: побываем в «деревне Исторической», посетим «замок Кроссвордный», заглянем на «Тестодром», поиграем на «Поле чудес», отдохнём на «поляне Правил», одолеем «горы Ума», побродим в «лесу Сказочном». На каждой остановке вам надо будет показать свои знания правил сложения, вычитания, умножения и деления обыкновенных дробей, умение применять их при решении задач и уравнений, проявить активность, находчивость и смекалку. За правильные ответы вы получите оценки. 2)Попасть в страну Обыкновенные дроби, минуя «Деревню Историческую» нельзя. Поэтому первую остановку мы сделаем здесь, где вам расскажут об истории возникновения дробей. Сообщение учащихся: «История возникновения обыкновенных дробей». ![c:\documents and settings\1\рабочий стол\рисунки\i[36].jpg](1029727_html_m12ed62a4.jpg) 3.Воспроизведение и коррекция опорных знаний, повторение и анализ основных фактов 1)Следующая остановка «Замок Кроссвордный», здесь учащимся нужно отгадать кроссворд. По вертикали: 1.Как называется дробь, записанная в виде 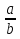 ? ?По горизонтали: 2.Как называется число, записанное над чертой дроби? 3. Как называется число, записанное под чертой дроби? 4.Как называется дробь, у которой числитель и знаменатель делятся на одно и то же число? 5. Как называется дробь, у которой числитель меньше знаменателя? 6. Как называется дробь, у которой числитель больше или равен знаменателю? Кроссворд:
Кроссворд (ответы)
2) А сейчас заглянем на «Тестодром», где учащиеся должны устно найти и показать правильные ответы на вопросы, подняв соответствующую сигнальную карточку. Тест:
4.Обобщение и систематизация знаний и их применение при выполнении практических заданий. 1) На «Поле Чудес» учащимся надо расшифровать фразу. Каждый ученик вычисляет значение выражения записанного на карточке, записывает соответствующую найденному числу букву из таблицы под номером своей карточки. Разно-уровневые карточки:
Ответы:
Фраза:
2)Сейчас отдохнём на «Поляне Правил», сделаем зарядку и нарвём цветов. Но цветы на ней необыкновенные. Каждый цветок – это правило по теме урока. Вопросы задают учащиеся, а двое учеников по очереди на них отвечают. 5.Проверка умений учащихся самостоятельно применять знания. Чтобы одолеть «Горы Ума» надо выполнить самостоятельную работу. ![c:\documents and settings\1\рабочий стол\рисунки\confused[1].jpg](1029727_html_m7481979a.jpg) Дифференцированные карточки:
6.Домашнее задание: усвоение ведущих идей и основных теорий. Последняя остановка в «Лесу Сказочном». Учащимся предлагается дома выполнить №925(б;в), составить кроссворд или написать сказку о «стране Обыкновенные дроби». 7.Подведение итогов урока. В заключении замечу, развитие учащихся в процессе обучения математике определяется характером организации работы, превращения учения в учебную деятельность. Это значит, что при изучении математики не формулирую готовые факты, не навешиваю новые знания и умения, а создаю условия, при которых ученики с помощью своих одноклассников и учителя разворачивают учебный материал, упорядочивают его, прогнозируют направление его развития, формулируют ту учебную задачу, которую им нужно решить. Одновременно учебный материал для ученика предстаёт не в статичном виде, а становится понятным необходимость введения новых понятий, исследование их свойств, взаимосвязь с другими науками, с житейской практикой. Знание становится «живым», что позволяет создать условия для саморазвития ученика. |
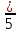 была правильной?
была правильной?
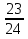 ; 2)
; 2)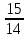 ; 3)
; 3)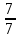 .
.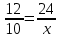 верно?
верно?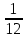 +
+ 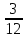 )∙ 9.
)∙ 9.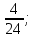 2)
2) 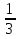 ; 3) 3.
; 3) 3.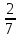 =1.
=1.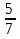 ; 2)
; 2)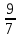 ; 3)
; 3)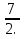
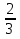 от числа 12.
от числа 12.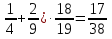
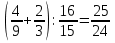
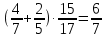
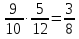
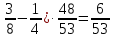
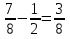
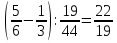
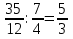
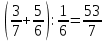
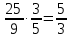
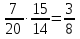
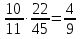
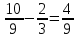
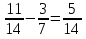
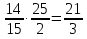
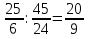
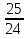
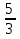
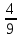
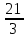
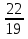
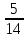
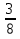
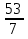
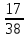
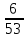
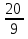
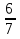
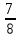 -
- 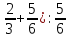 .
. 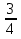 метра меньшепервой.
метра меньшепервой.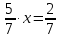 .
.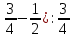 .
.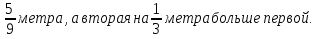
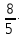 х =
х = 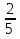 .
.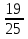 -
- 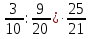 .
.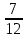
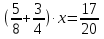 .
.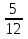 +
+ 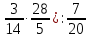 .
.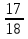
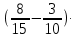 х =
х = 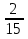 .
.