Пирцхалава Светланы Алексеевны Высшая квалификационная категория Москва 2014 пояснительная записка рабочая программа
 Скачать 468.58 Kb. Скачать 468.58 Kb.
|
7.Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре.1. Оценка письменных контрольных работ обучающихся по алгебре.Ответ оценивается отметкой «5», если:
Отметка «4» ставится в следующих случаях:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий. 2. Оценка устных ответов обучающихся по алгебре.Ответ оценивается отметкой «5», если ученик:
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
Отметка «3» ставится в следующих случаях:
Отметка «2» ставится в следующих случаях:
Контрольная работа разделена на две части: до черты – задания обязательного уровня, после черты – задания более высокого уровня. Контрольные работы по алгебре и началам математического анализа 11 класс Контрольная работа № 1 Тема: «Первообразная»
а). F(x) = x4 – 3, f(x) = 4x3. б). F(x) = 5x – cosx, f(x) = 5 + sinx.
а). f(x) = б). f(x) = x2(1 – x). __________________________________________________________________ в). f(x) = 4 sinxcosx.
Контрольная работа № 2. Тема: «Интеграл»
а). 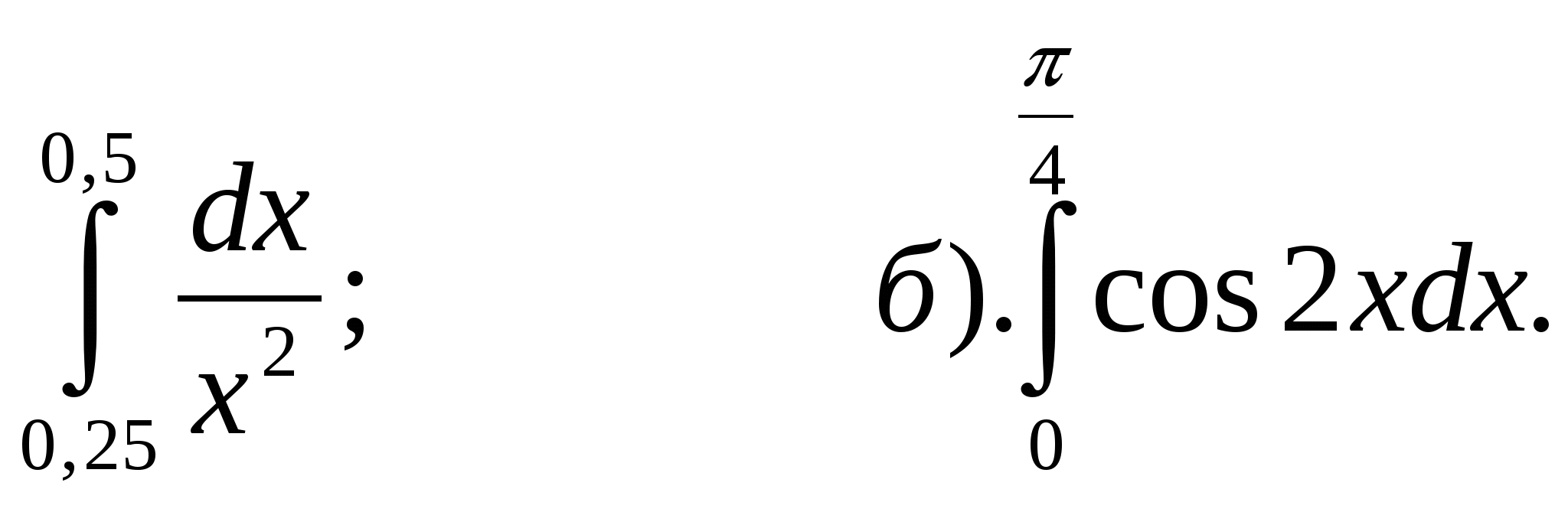
________________________________________________________________________
а) касательной к этому графику в его очке с абсциссой х = -2 и прямой х = 0; б) касательными к этому графику в его точках с абсциссами х = -2 и х = 2. Контрольная работа № 3. Тема: «Обобщение понятия степени» 1. Упростите выражение: 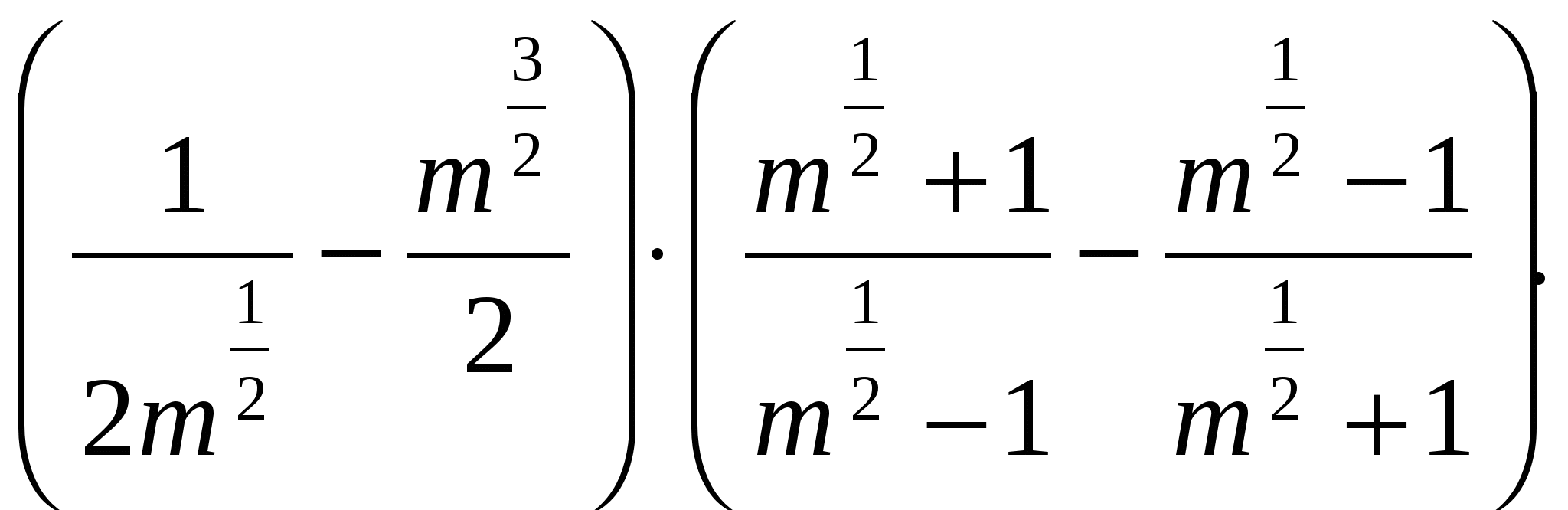 2. Решите уравнение ___________________________________________________________________________ 3. Решите систему уравнений 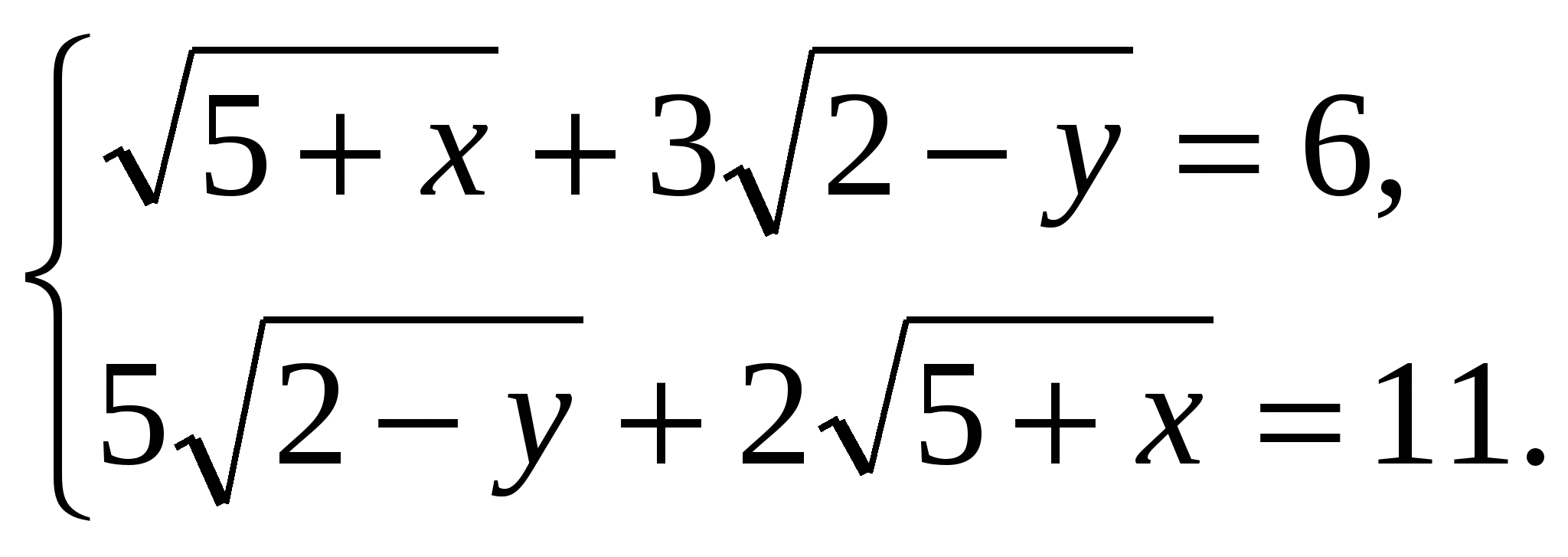 4. Решите неравенство Контрольная работа № 4. Тема: «Показательная и логарифмическая функции».
а). постройте график этой функции; б). Опишите свойства этой функции.
_________________________________________________________________________________ 5. Решите уравнение 6. Решите систему уравнений: 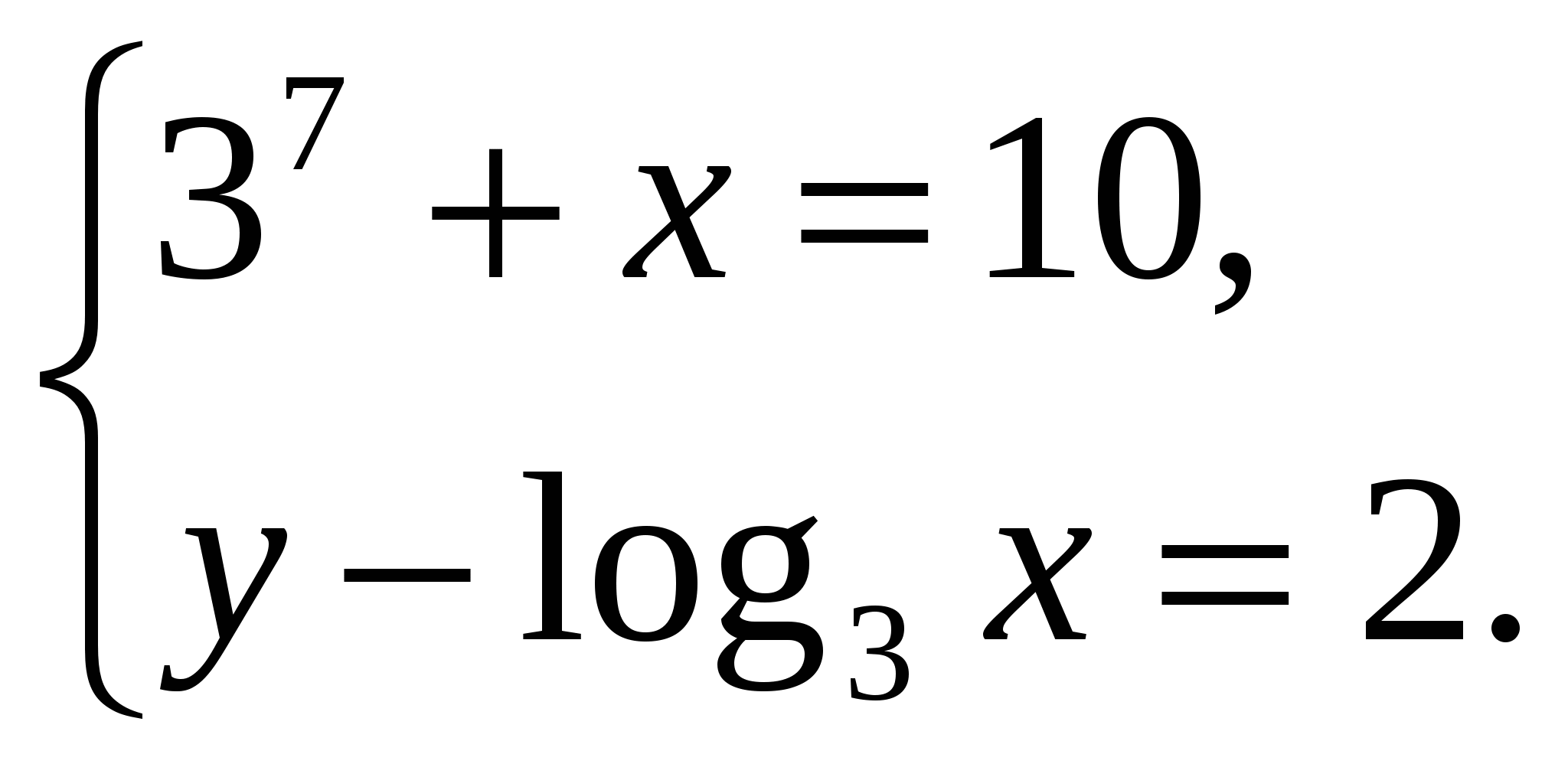 Контрольная работа № 5. Тема: «Производная показательной и логарифмической функций». 1. Найдите 2. Докажите, что функция у = cos(4x -1) является решением дифференциального уравнения у” = - 16у. 3. Составьте уравнение касательной, проведенной к графику функции у = е _________________________________________________________________________________ 4. Найдите промежутки возрастания и убывания функции у = 2хех. 5. Вычислите площадь фигуры, ограниченной линиями Каждая контрольная работа разделена на две части: до черты – задания обязательного уровня, после черты – задания более высокого уровня. Оценивание контрольных работ (утверждено на заседании школьного методического объединения учителей математики ) Оценка "5"ставится: а) работа выполнена полностью и без ошибок; б) количество недочетов в такой работе не должно превышать двух. Оценка "4" ставится: а) работа выполнена полностью, но содержит не более 3-4 недочетов; б) из всех предложенных заданий не выполнено одно задание; в) содержит одну грубую ошибку. Оценка "3" ставится: а) выполнено верно половина из всех предложенных заданий б) работа содержит не более 5-7 недочетов. Оценка "2" ставится во всех остальных случаях. Грубые ошибки. К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять, незнание приемов решения задач, рассматриваемых в учебных пособиях, а также вычислительные ошибки, если он не являются опиской. Негрубые ошибки - потеря корня или сохранение в ответе постороннего корня; - отбрасывание без объяснения одного из корня и равнозначные им. К недочетам относятся: - нерациональное решение, описки, недостаточность; - отсутствие пояснений, обоснований в решениях. Если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет). Зачеркивание в работе (желательно, чтобы они были аккуратными) свидетельствует о поисках решения, что считать ошибкой не следует. 8.Список литературы и ресурсное обеспечение: 1.Настольная книга учителя математики. М.: ООО «Издательство АСТ»: ООО «Издательство Астрель», 2004; 2.Методические рекомендации к учебникам математики для 10-11 классов, журнал «Математика в школе» №2-2005год; 3.Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразоват. учреждений /А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004. 4.Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003. 5.Алгебра и математический анализ, под редакцией Н. Я. Виленкина, - М. Просвещение, 2001. 6.«Алгебра и начала анализа 11кл.» Г.К.Муравин, О.В.Муравина. Дрофа. 2004г. 7.Программа курса математики для общеобразовательной школы «Математика 5-11кл.» Г.К.Муравин, О.В.Муравина. Дрофа. 2007г.
1 Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников. | |||||||||||||||||