|
Пояснительная записка Программа по математике составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне
Пояснительная записка
Программа по математике составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования на базовом уровне.
Программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.
Программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Общая характеристика учебного предмета
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
— систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
— развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
— систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
— расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
— развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
— совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
— формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Цели
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:
— проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
— решения широкого класса задач из различных разделов курса; поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
— планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнения расчетов практического характера;
— построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
— самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
Главу «Некоторые сведения из планиметрии» планирую изучить в конце года. Считаю, что это положительно повлияет на знания учащихся.
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
Повторение (4 ч)
Основная цель – формирование представлений о целостности и непрерывности курса математики 10 класса. Овладение умением обобщения и систематизации знаний учащихся по основным темам курса математики 10 класса. Развитие логического, математического мышления и интуиции, творческих способностей в области математики.
Многочлены (10ч)
Многочлены от одной и нескольких переменных. Теорема Безу. Схема Горнера. Симметрические и однородные многочлены. Уравнения высших степеней.
Основная цель – формирование представлений о понятии многочлена от одной и нескольких переменных, об уравнениях высших степеней. Овладение навыками арифметических операций над многочленами, деления многочлена на многочлен с остатком, разложения многочлена на множители.
Овладение умением решения разными методами уравнений высших степеней.
Знать:
- алгоритм действий с многочленами; способы разложения многочлена на множители;
-Уметь:
- выполнять действия с многочленами; находить корни многочлена с одной переменной раскла-дывать многочлены на множители.
Степени и корни. Степенные функции ( 24ч)
Понятие корня n-ой степени из действительного числа. Функции 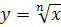 , их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел. , их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел.
Основная цель - формирование представлений корня n-ой степени из действительного числа, степенной функции и графика этой функции.
Овладение умением извлечения корня, построения графика степенной функции и определения свойств функции. Овладение навыками упрощения выражений, содержащих радикал, применяя свойства корня. Обобщение и систематизация знания о степенной функции, о свойствах и графиках степенной функции в зависимости от значений оснований и показателей степени.
Знать:
- свойства корня n-ой степени; свойства функции 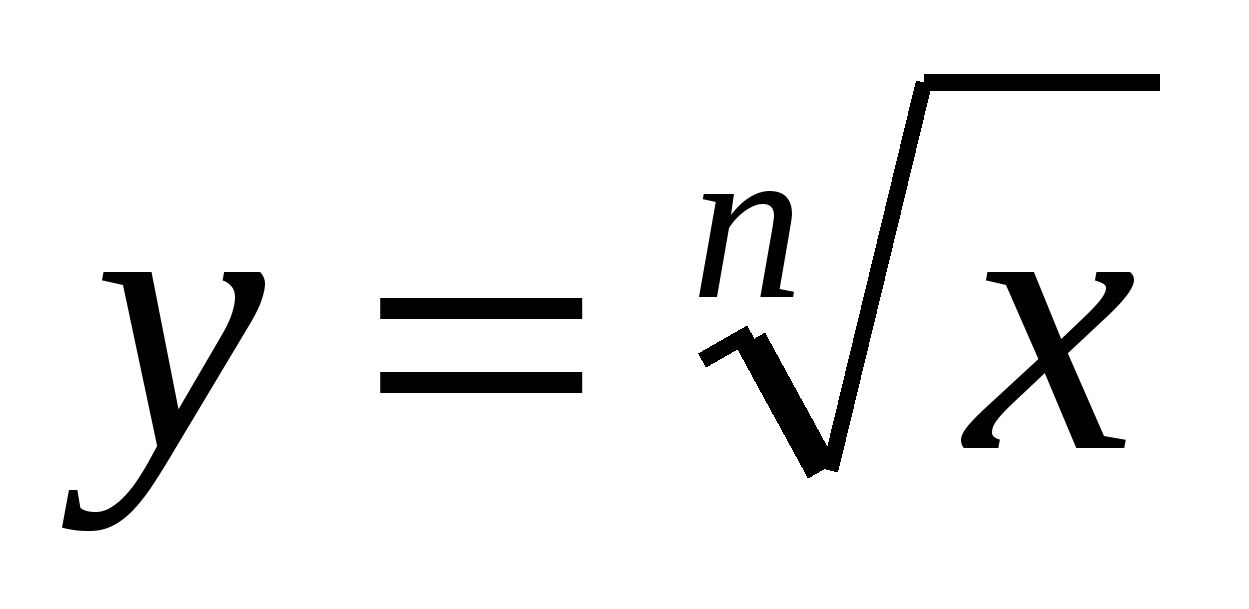 ; определение степени с рациональным показателем; свойства степенных функций. ; определение степени с рациональным показателем; свойства степенных функций.
Иметь представление о формуле для извлечения корня n-ой степени из комплексного числа.
Уметь:
- находить значение корня натуральной степени; проводить преобразования числовых и буквенных выражений, содержащих радикалы; пользоваться оценкой и прикидкой при практических расчетах; строить графики функции 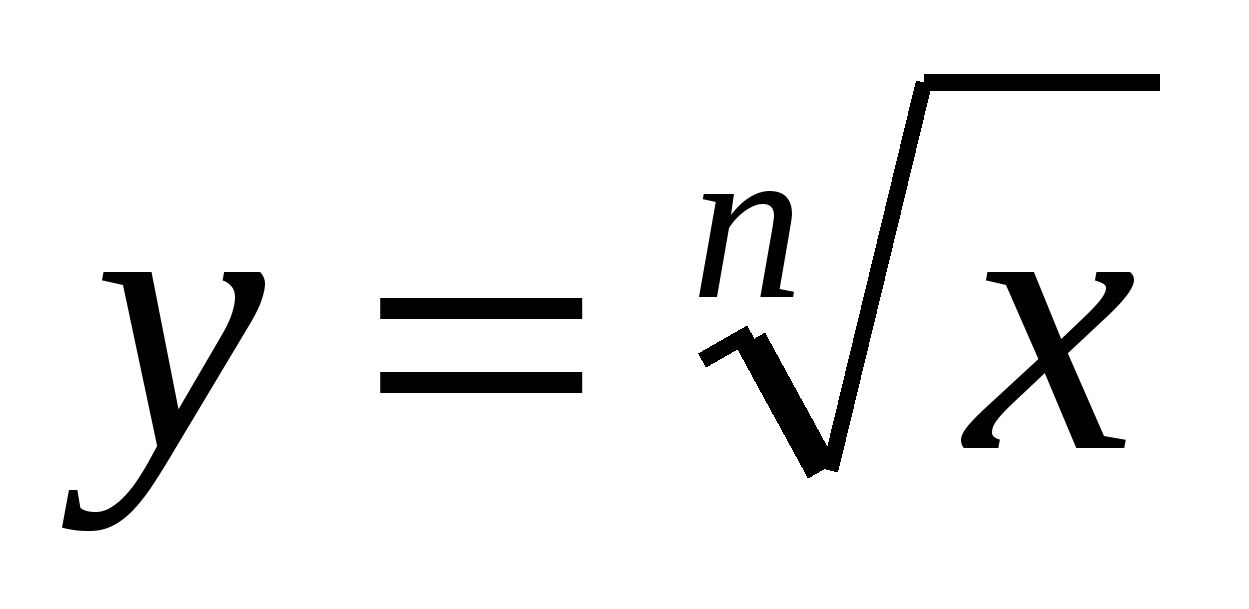 , выполнять преобразования графиков; , выполнять преобразования графиков;
решать уравнения и неравенства, используя свойства функции 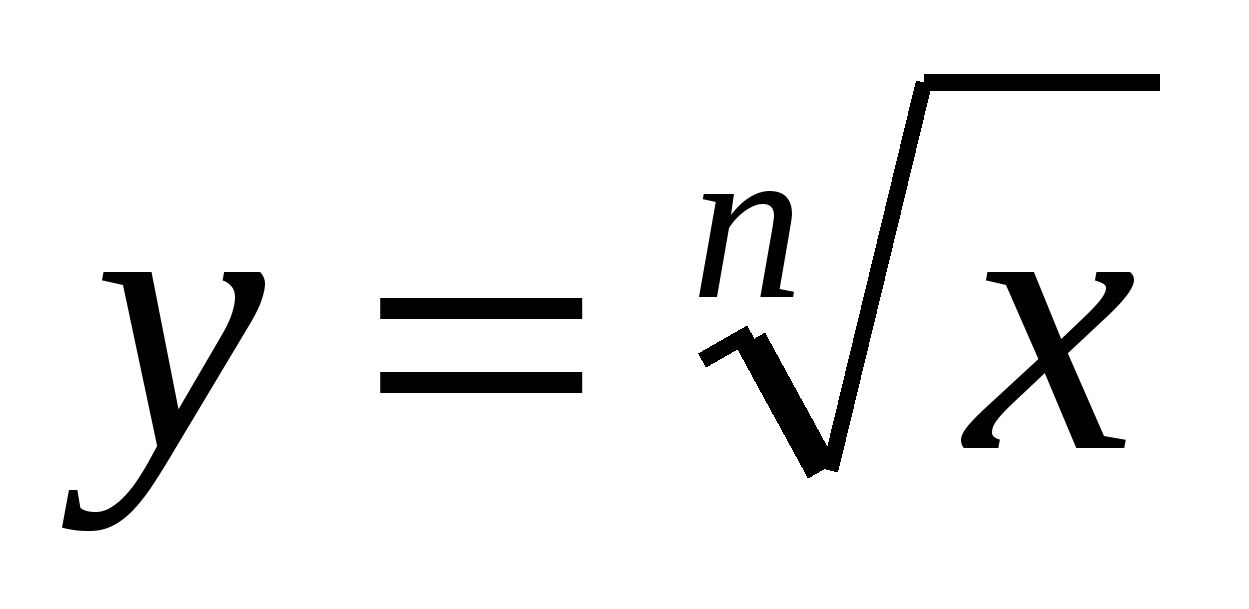 и ее графическое представление; находить значение степени с рациональным показателем; проводить преобразования числовых и буквенных выражений, содержащих степени; строить графики степенных функций, выполнять преобразования графиков; описывать по графику и формуле свойства степенной функции; решать уравнения и неравенства, используя свойства степенных функции и их графическое представление. и ее графическое представление; находить значение степени с рациональным показателем; проводить преобразования числовых и буквенных выражений, содержащих степени; строить графики степенных функций, выполнять преобразования графиков; описывать по графику и формуле свойства степенной функции; решать уравнения и неравенства, используя свойства степенных функции и их графическое представление.
Показательная и логарифмическая функции (31ч)
Показательная функция, ее свойства и график. Показательные уравнения и неравенства. Понятие логарифма. Функция 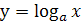 , ее свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Дифференцирование показательной и логарифмической функций. , ее свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Дифференцирование показательной и логарифмической функций.
Основная цель - формирование представлений о показательной и логарифмической функциях, их графиках и свойствах. Овладение умением понимать и читать свойства и графики логарифмической функции, решать логарифмические уравнения и неравенства . Овладение умением понимать и читать свойства и графики показательной функции, решать показательные уравнения и неравенства. Развитие умения применять функционально-графические представления для описания и анализа закономерностей, существующих в окружающем мире и в смежных предметах.
Знать:
- определение показательной функции; свойства показательной функции; способы решения показательных уравнений и неравенств; определение логарифма; свойства логарифмической функции; способы решения логарифмических уравнений и неравенств; определение натурального логарифма; формулы производных показательной и логарифмической функций.
Уметь:
- находить значение логарифмов; строить графики логарифмической и показательной функций, выполнять преобразования графиков; описывать по графику и формуле свойства логарифмической и показательной функций; решать уравнения и неравенства, используя свойства показательных и логарифмических функции и их графическое представление; решать показательные и логарифмические уравнения и неравенства и их системы; проводить преобразования выражений, содержащих логарифмы; вычислять производные показательной и логарифмической функций.
Интеграл (9ч)
Первообразная и неопределенный интеграл. Определенный интеграл, его вычисление и свойства. Вычисление площадей плоских фигур. Примеры применения интеграла в физике.
Основная цель - формирование представлений о понятиях первообразной, неопределенного интеграла, определенного интеграла. Овладение умением применения первообразной функции при решении задачи вычисления площадей криволинейных трапеций и других плоских фигур.
Знать:
- определение первообразной; правила отыскания первообразных; формулы первообразных элементарных функций; определение криволинейной трапеции.
Уметь:
- вычислять первообразные элементарных функций, применяя правила вычисления первообразных; вычислять площадь криволинейной трапеции.
Элементы комбинаторики, статистики и теории вероятностей (9ч)
Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки информации. Гауссова кривая. Закон больших чисел. Формулы сложения, приведения, двойного аргумента, понижения степени.
Основная цель - формирование первичных представлений о комбинаторных задачах, статистических методов обработки информации, независимых повторений испытаний в вероятностных заданиях. Овладение умением применения классической вероятностной схемы, схемы Бернулли, закона больших чисел. Развитие понимания, что реальный мир подчиняется не только детерминированным, но и статистическим закономерностям и умения использовать их для решения задач повседневной жизни .
Знать:
- правило геометрических вероятностей; вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения; понятия: общий ряд данных, выборка, варианта, кратность варианты, таблица распределения, частота варианты, график распределения частот; способы представления информации; график, какой функции называется гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях; закон больших чисел.
Уметь:
- решать простейшие комбинаторные задачи с использование известных формул;
использовать знания в практической деятельности для анализа числовых данных, представленных в виде диаграмм и графиков; для анализа информации статистического характера.
Уравнения и неравенства. Системы уравнений и неравенств (33ч)
Равносильность уравнений. Общие методы решения уравнений. Уравнения с модулями. Иррациональные уравнения. Доказательство неравенств. Решение рациональных неравенств с одной переменной. Неравенства с модулями. Иррациональные неравенства. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Системы уравнений. Уравнения и неравенства с параметрами.
Основная цель - формирование представлений об уравнениях, неравенствах и их системах, о решении уравнения, неравенства и системы, о уравнениях и неравенствах с параметром. Овладение навыками общих методов решения уравнений, неравенств и их систем. Овладение умением решения уравнений и неравенств с параметрами, нахождения всех возможных решений, в зависимости от значения параметра; обобщение и систематизация имеющихся сведений об уравнениях, неравенствах, системах и методах их решения; познакомиться с общими методами решения. Развитие умения проводить аргументированные рассуждения, делать логически обоснованные выводы, отличать доказанные утверждения от недоказанных, ясно, точно и грамотно выражать свои мысли в устной и письменной речи.
Знать:
- определение равносильности уравнений и неравенств; способы решения уравнений и систем уравнений; понятия системы и совокупности неравенств.
Уметь:
-решать уравнения, неравенства и системы с применением графических представлений и свойств функций; доказывать несложные неравенства; изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем
Метод координат в пространстве. Движения (15ч)
Координаты точки и координаты вектора. Прямоугольная система координат в пространства. Координаты вектора. Связь между координатами векторов и координатами точек. Простейшие задачи в координатах. Угол между векторами. Скалярное произведение векторов. Вычисление углов между прямыми и плоскостями. Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.
Основная цель - формирование представлений о прямоугольной системе координат в пространстве, о координатном и векторном методах решения простейших задач. Овладение умением применять координатный и векторный методы к решению задач на нахождение длин отрезков и углов между прямыми и векторами в пространстве. Овладение умением проводить доказательные рассуждения в ходе решения стереометрических задач.
Знать:
-алгоритмы: разложения векторов по координатным векторам; сложения двух и более векторов; произведения вектора на число; разности двух векторов; признаки коллинеарности и компланарности векторов; формулы: координат середины отрезка; длины вектора; расстояния между двумя точками; формулу нахождения скалярного произведения векторов.
Иметь представление: об угле между векторами, скалярном квадрате вектора; о каждом из видов движения.
Уметь:
- строить точки по их координатам, находить координаты векторов; находить сумму и разность векторов, применять формулы: координат середины отрезка; длины вектора; расстояния между двумя точками для решения задач координатно-векторным способом; находить угол между прямой и плоскостью; уметь выполнять построение фигуры, симметричной относительно оси симметрии, центра симметрии, плоскости, при параллельном переносе.
Цилиндр, конус, шар (17ч)
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усеченный конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.
Основная цель - формирование представлений о телах вращения: цилиндре, конуса, усеченного конуса, сферы и шара. Овладение умением находить площади поверхностей тел вращения. Овладение навыками решения задач на многогранники и тела вращения. Овладение умением проводить доказательные рассуждения в ходе решения стереометрических задач.
Знать:
- формулы площадей боковой и полной поверхностей цилиндра. элементы конуса; элементы усеченного конуса; формулы площади боковой и полной поверхности конуса и усеченного конуса; определение сферы и шара; свойства касательной к сфере; уравнение сферы; формулу площади сферы.
Уметь:
- выполнять чертежи по условию задачи; строить осевое сечение цилиндра и находить его площадь; решать задачи на нахождения площади боковой и полной поверхности цилиндра.
уметь выполнять построение конуса и усеченного конуса и их сечений; находить элементы конуса и усеченного конуса; решать задачи на нахождение площади поверхности конуса и усеченного конуса; определять взаимное расположение сфер и плоскости; составлять уравнение сферы по координатам точек; уметь решать типовые задачи на нахождение площади сферы.
Объемы тел (22ч)
Понятие объема. Объем прямоугольного параллелепипеда. Объем прямой призмы. Объем цилиндра. Вычисление объемов тел с помощью интеграла. Объем наклонной призмы. Объем пирамиды. Объем конуса. Объем шара. Объемы шарового сегмента, шарового слоя, шарового сектора. Площадь сферы. Задачи на многогранники, цилиндр, конус и шар.
Основная цель - формирование представлений о понятии объема многогранника и тела вращения. Обобщение и систематизация сведения о многогранниках и телах вращения в ходе решения задач на вычисление их объемов. Создание условия для использования при решении стереометрических задач планиметрические факты и методы. Овладение умением проводить доказательные рассуждения в ходе решения стереометрических задач.
Знать:
- формулы объемов прямоугольного параллелепипеда, прямой и наклонной призм, цилиндра, конуса, шара; знать метод вычисления объема через определенный интеграл; формулу площади сферы. Иметь представление шаровом сегменте, шаровом секторе, слое.
Уметь:
- решать задачи на нахождение объемов; решать задачи на вычисление площади сферы.
Обобщающее повторение (18 +14 ч)
Основная цель - уметь использовать приобретенные знания и умения в практической деятельности для решения задач разного уровня сложности на основе изученного материала. Уметь использовать приобретенные знания и умения в практической деятельности для решения задач на основе изученных формул и свойств фигур.
Учебно-тематический план
Повторение (6 ч)
Многочлены (10ч)
Степени и корни. Степенные функции ( 24ч)
Показательная и логарифмическая функции (31ч)
Первообразная и интеграл (9ч)
Элементы комбинаторики, статистики и теории вероятностей (9ч)
Уравнения и неравенства. Системы уравнений и неравенств (31ч)
Метод координат в пространстве. Движения (15ч)
Цилиндр, конус, шар (17ч)
Объемы тел (22ч)
Обобщающее повторение (30 ч)
Требования к знаниям, умениям и навыкам учащихся
В результате изучения математики на профильном уровне ученик должен знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностных характер различных процессов и закономерностей окружающего мира;
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
Начала математического анализа
уметь
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи);
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Геометрия
уметь
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Перечень учебно-методического обеспечения
Программа «Алгебра и начала математического анализа 10-11 классы» для общеобразовательных учреждений: для классов, изучающих предмет на базовом, предпрофильном и профильном уровнях. Составитель И. И. Зубарева, А. Г. Мордкович. – М.: «Мнемозина», 2011 г.
Программа общеобразовательных учреждений «ГЕОМЕТРИЯ 10-11 классы». Составитель: Т.А. Бурмистрова. Москва «Просвещение», 2011 год.
Поурочные разработки к учебнику «Геометрия» 11 класс В. Я. Яровенко Москва ВАКО 2011 г
Учебник:
А. Г. Мордкович, Алгебра и начало анализа. 11 класс. Часть 1. Учебник для общеобразовательных учреждений (профильный уровень). - М.: Мнемозина, 2013 г.
А. Г. Мордкович и др. Алгебра и начала анализа. 11 класс. Часть 2. Задачник для общеобразовательных учреждений (профильный уровень). - М.: Мнемозина, 2013 г.
Учебник:
Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Геометрия, 10-11. Учебник для общеобразовательных учреждений: базовый и профильный уровни.- М.: Просвещение, 2013 г.
Дополнительная литература:
«Алгебра: Элементы статистики и теории вероятностей» Макарычев Ю. Н., Миндюк Н. Г.
«Тесты по алгебре и началам анализа» Н. А. Глазков, И. К. Варшавский и др. 2010 г.
А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская Алгебра и начала анализа 10–11 классы. Задачник – М: Мнемозина 2007, 2007 г.;
А. Г. Мордкович Алгебра и начала анализа 10–11 классы. Пособие для учителей М.: Мнемозина 2004 г.;
А. Г. Мордкович, Е. Е. Тульчинская Алгебра и начала анализа 10–11 классы. Контрольные работы - М.: Мнемозина 2005 г.;
Тематическое планирование по математике 10 класс
Дата провед урока план.
|
Дата провед урока факт.
|
№ п/п
|
№ п/п
|
Глава
|
Тема урока
|
Требования к уровню подготовки учащихся
|
Тип урока
|
3.09
|
|
|
1
|
Метод координат в пространстве
|
Прямоугольная система координат в пространстве
|
Иметь представление о прямоугольной системе координат в пространстве. Уметь строить точку по заданным координатам и находить координаты точки, изображенной в заданной системе координат.
|
Изучение нового материала
|
4.09
|
|
|
1
|
Повторение материала, изученного в 10 классе
|
Повторение материала, изученного в 10 классе
|
Уметь работать с дей-ствительными числами. Знать числовые функции.
|
Комбинированный урок
|
5.09
|
|
|
2
|
|
Повторение материала, изученного в 10 классе
|
Уметь преобразовывать простые тригонометрические выражения, решать простые тригонометрические уравнения.
|
Урок закрепления знаний и умений.
|
6.09
|
|
|
2
|
|
Координаты вектора
|
Знать определение понятия координат вектора в пространстве. Уметь выполнять действия над векторами с заданными координатами; раскладывать вектор по базису.
|
Комбинированный
|
7.09
|
|
|
3
|
|
Повторение материала, изученного в 10 классе
|
Уметь преобразовывать простые тригонометрические выражения, решать простые тригонометрические уравнения.
|
Комбинированный урок
|
9.09
|
|
|
4
|
|
Повторение материала, изученного в 10 классе
|
Уметь находить производные суммы, разности, произведения, частного; производные основных элементарных функций.
|
Комбинированный урок
|
10.09
|
|
|
3
|
|
Координаты вектора
|
Знать определение понятия координат вектора в пространстве. Уметь выполнять действия над векторами с заданными координатами; раскладывать вектор по базису.
|
Учебный практикум
|
11.09
|
|
|
5
|
Многочлены (10)
|
Многочлены от одной переменной.
|
Уметь выполнять арифметические операции над многочленами от одной переменной.
|
Урок изучения нового материала
|
12.09
|
|
|
6
|
|
Многочлены от одной переменной.
|
Уметь выполнять арифметические операции над многочленами от одной переменной.
|
Урок изучения нового материала
|
13.09
|
|
|
4
|
|
Связь между координатами векторов и координатами точек
| Знать определение радиус- вектора произвольной точки пространства; знать определение коллинеарных и компланарных векторов. Уметь находить координаты вектора по координатам его начала и конца. |
Комбинированный
|
14.09
|
|
|
7
|
|
Многочлены от одной переменной.
|
Уметь выполнять арифметические операции над многочленами от одной переменной.
|
Урок изучения нового материала
|
16.09
|
|
|
8
|
|
Многочлены от нескольких переменных
|
Уметь решать различными способами задание с одно-родными и симметричес-кими многочленами от нескольких переменных
|
Комбинированный урок
|
17.09
|
|
|
5
|
|
Простейшие задачи в координатах
| Знать формулы координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками. Уметь применять эти формулы при решении стереометрических задач. |
Комбинированный
|
18.09
|
|
|
9
|
|
Многочлены от нескольких переменных
|
Уметь решать различными способами задание с однородными и симметрическими многочленами от нескольких переменных
|
Урок изучения нового материала
|
19.09
|
19.09
|
|
10
|
|
Многочлены от нескольких переменных
|
Уметь строить графики уравнений, содержащих две переменные
|
Комбинированный урок
|
20.09
|
20.09
|
|
6
|
|
Простейшие задачи в координатах
| Знать формулы координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками. Уметь применять эти формулы при решении стереометрических задач. |
Учебный практикум
|
21.09
|
21.09
|
|
11
|
|
Уравнения высших степеней.
|
Уметь использовать различные функционально-графические приемы. возвратных уравнений.
|
Урок изучения нового материала
|
23.09
|
|
|
|
|
Уравнения высших степеней.
|
Уметь использовать различные функционально-графические приемы. возвратных уравнений.
|
Урок изучения нового материала
|
24.09
|
20.09
|
|
7
|
|
Простейшие задачи в координатах Контрольная работа №1
|
Демонстрация учащимися навыков использования формул для решения задач векторно-координатным методом.
|
Урок проверки знаний и умений
|
25.09
|
|
|
12
|
|
Уравнения высших степеней.
|
Уметь использовать различные функционально-графические приемы. возвратных уравнений.
|
Комбинированный урок
|
26.09
|
|
|
13
|
|
Контрольная работа по теме «Многочлены»
|
Уметь делить многочлены, раскладывать многочлены на множители, решать уравнения высших степеней.
|
Урок проверки знаний и умений
|
27.09
|
24.09
|
|
8
|
Скалярное произведение векторов. (4 ч.)
|
Угол между векторами. Скалярное произведение векторов
|
Знать понятие угла между векторами и скалярного произведения векторов; знать формулу скалярного произведения в координатах, свойства скалярного произведения.
Уметь применять скалярное произведение при решении задач
|
Изучение нового материала
|
28.09
|
|
|
14
|
Степени и корни . Степенные функции.
|
Понятие корня n-й степени из действительного числа.
|
Уметь определять корень n-й степени, арифметический корень n-й степени, основные свойства.
|
Урок изучения нового материала
|
30.09
|
|
|
15
|
|
Понятие корня n-й степени из действительного числа.
|
Уметь определять корень n-й степени, арифметический корень n-й степени, основные свойства.
|
Урок закрепления знаний и умений.
|
1.10
|
27.09
|
|
9
|
|
Угол между векторами. Скалярное произведение векторов
|
Уметь применять скалярное произведение при решении задач.
|
Учебный практикум
|
2.10
|
|
|
16
|
|
Функции 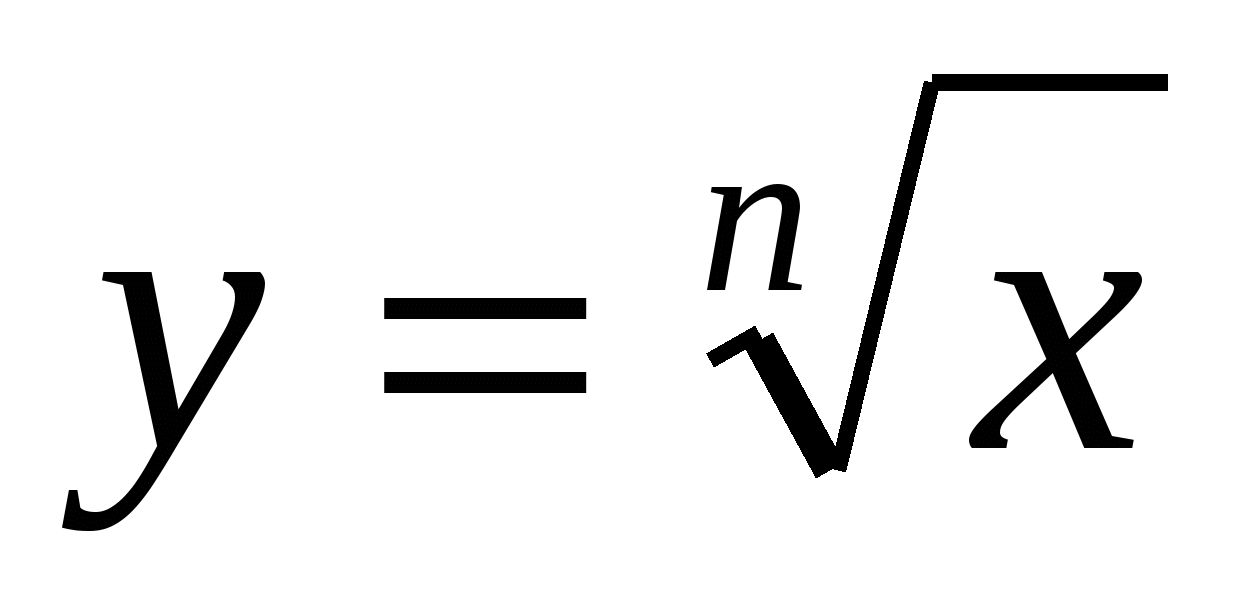 , их свойства и графики. , их свойства и графики.
|
Знать функции 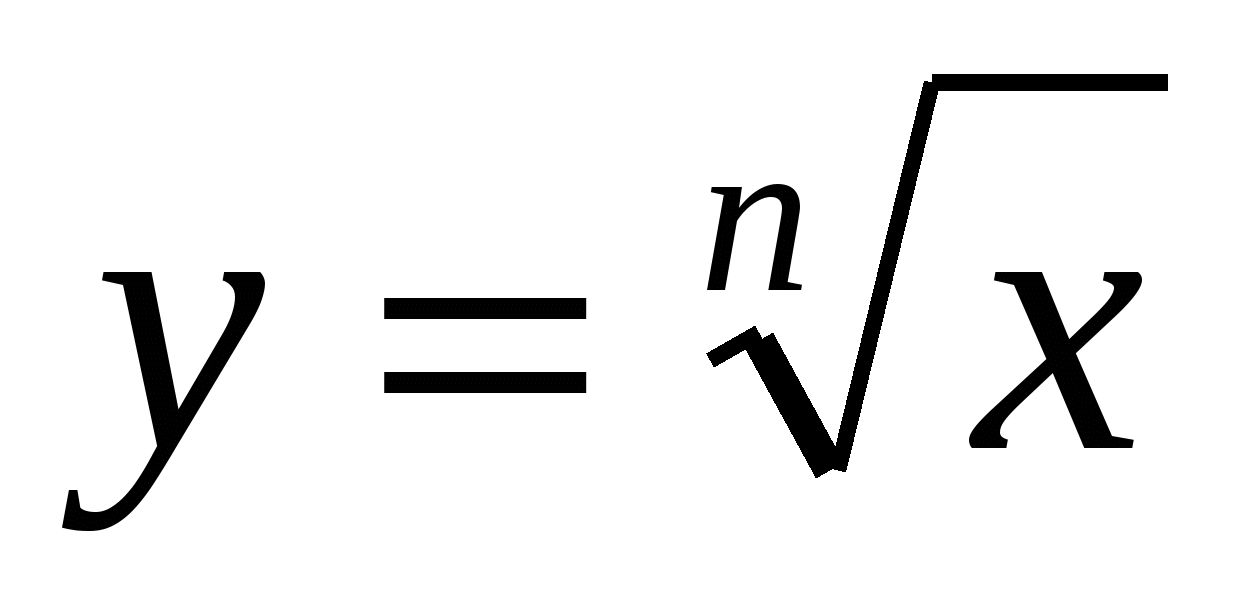 , их свойства и графики. Уметь строить графики функций , их свойства и графики. Уметь строить графики функций
|
Урок изучения нового материала
|
3.10
|
|
|
17
|
|
Функции 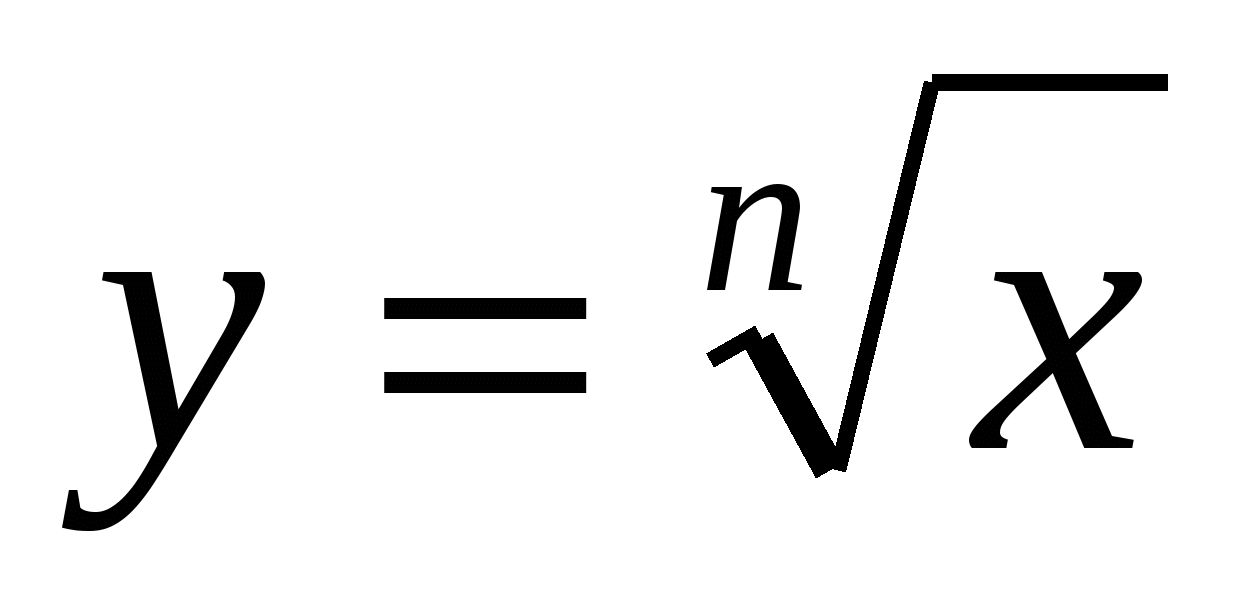 , их свойства и графики. , их свойства и графики.
|
Знать функции 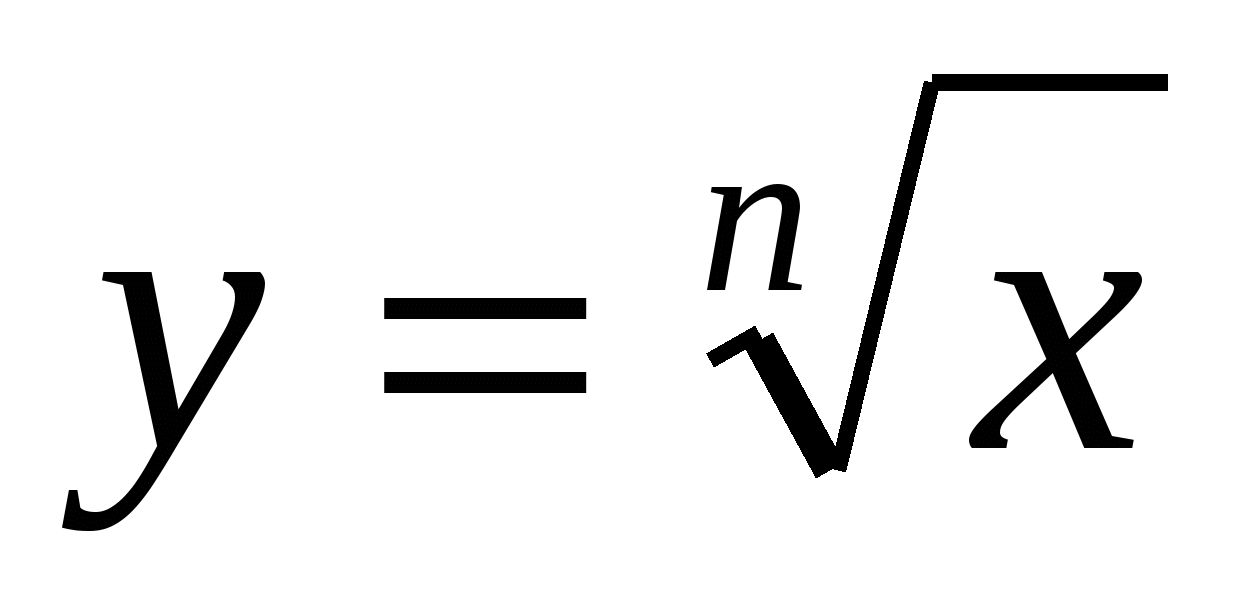 , их свойства и графики. Уметь строить графики функций , их свойства и графики. Уметь строить графики функций
|
Урок закрепления знаний и умений.
|
4.10
|
|
|
10
|
|
Вычисление углов между прямыми и плоскостями
|
Знать понятие угла между векторами и скалярного произведения векторов.
|
Комбинированный
|
5.10
|
|
|
18
|
|
Функции 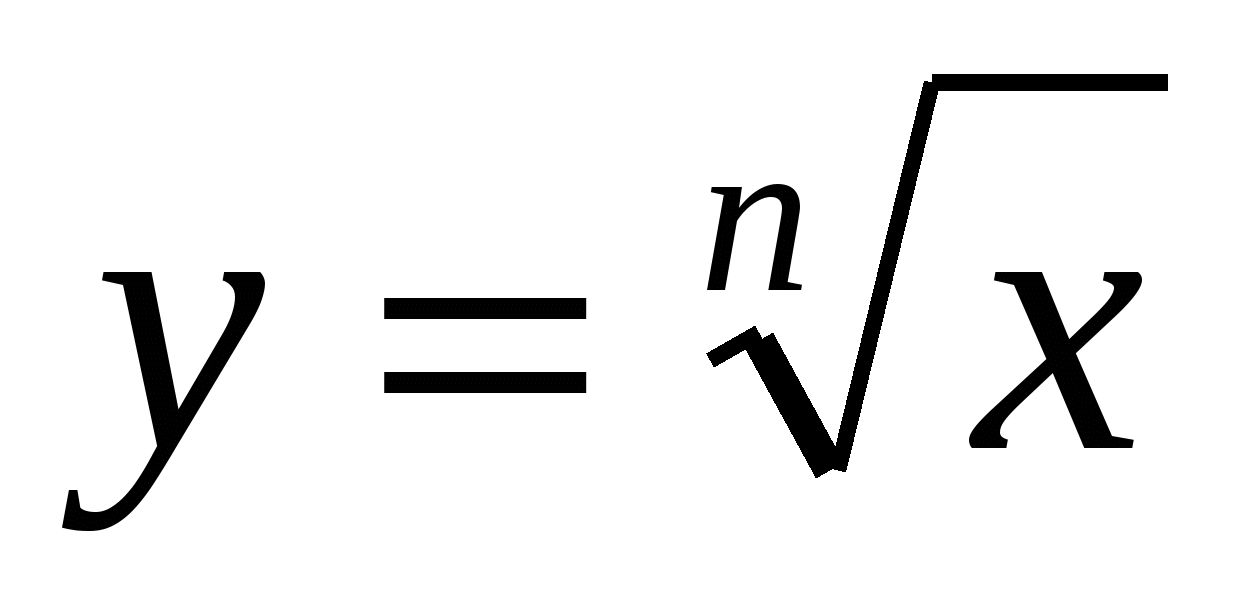 , их свойства и графики. , их свойства и графики.
|
Знать функции 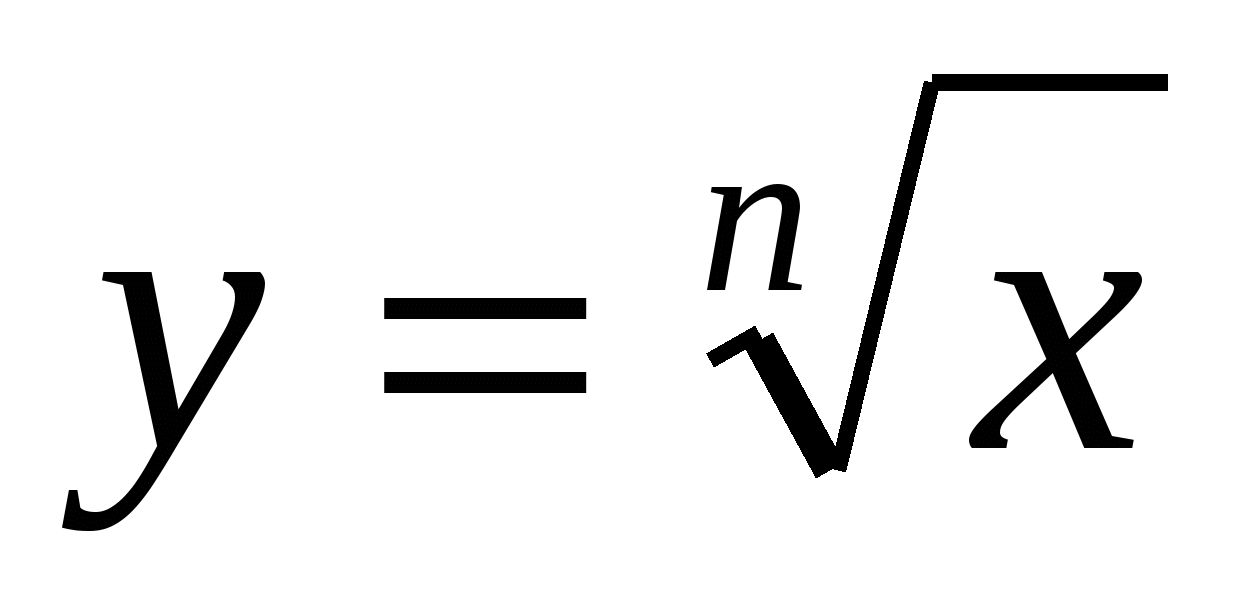 , их свойства и графики. Уметь строить графики функций , их свойства и графики. Уметь строить графики функций
|
Урок изучения нового материала
|
7.10
|
|
|
19
|
|
Свойства корня n-й степени
|
|
Урок изучения нового материала
|
8.10
|
|
|
11
|
|
Повторение вопросов теории, решение задач.
|
Знать формулу скалярного произведения в координатах, косинуса угла между данными векторами через их координаты, косинуса угла между прямыми, между прямой и плоскостью.
|
Учебный практикум
|
9.10
|
|
|
20
|
|
Свойства корня n-й степени
|
Уметь применять свойства корня n-й степени
|
Урок изучения нового материала
|
10.10
|
|
|
21
|
|
Свойства корня n-й степени
|
Уметь применять свойства корня n-й степени
|
Урок закрепления знаний и умений.
|
11.10
|
|
|
12
|
|
Движения. Центральная симметрия. Зеркальная симметрия. Осевая симметрия. Параллельный перенос.
|
Иметь понятие о движении в пространстве, знать основные виды движений, их свойства.
|
Учебный практикум
|
12.10
|
|
|
22
|
|
Преобразование выражений, содержащих радикалы
|
Уметь находить значение корна по известным правилам преобразования выражений
|
Урок закрепления знаний и умений.
|
14.10
|
|
|
23
|
|
Преобразование выражений, содержащих радикалы
|
Уметь находить значение корна по известным правилам преобразования выражений
|
Урок закрепления знаний и умений.
|
15.10
|
|
|
13
|
|
Решение задач по теме «Движения»
|
Уметь осуществлять виды движений; находить координаты точек при различных движениях
|
Учебный практикум
|
16.10
|
|
|
24
|
|
Преобразование выражений, содержащих радикалы
|
Уметь раскладывать на множители выражения содержащие знак радикала
|
Урок изучения нового материала
|
17.10
|
|
|
25
|
|
Преобразование выражений, содержащих радикалы
|
Уметь раскладывать на множители выражения содержащие знак радикала
|
Урок закрепления знаний и умений.
|
18.10
|
|
|
14
|
|
Контрольная работа №2 по тем: «Скалярное произведение векторов в пространстве. Движения.»
|
Демонстрация учащимися знаний и умений по теме «Метод координат в пространстве. Движения»
|
Контроль знаний и умений
| |
|
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.