Протокол № от 2012г. «Согласовано» Заместитель директора мбоу сош №3 /./. 2012г
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
______________________________________ 6. Решите уравнение Вариант 2 1. Вычислите: а) 2. Упростите выражение
4. Составьте уравнение касательной к графику функции в точке ___________________________________________________________ 5. Решите неравенство ______________________________________ 6. Решите уравнение Контрольная работа № 4 (2 ч) Вариант 1 1. Постройте график функции: а) 2. Решите уравнение: а) 3. Решите неравенство 4. Вычислите 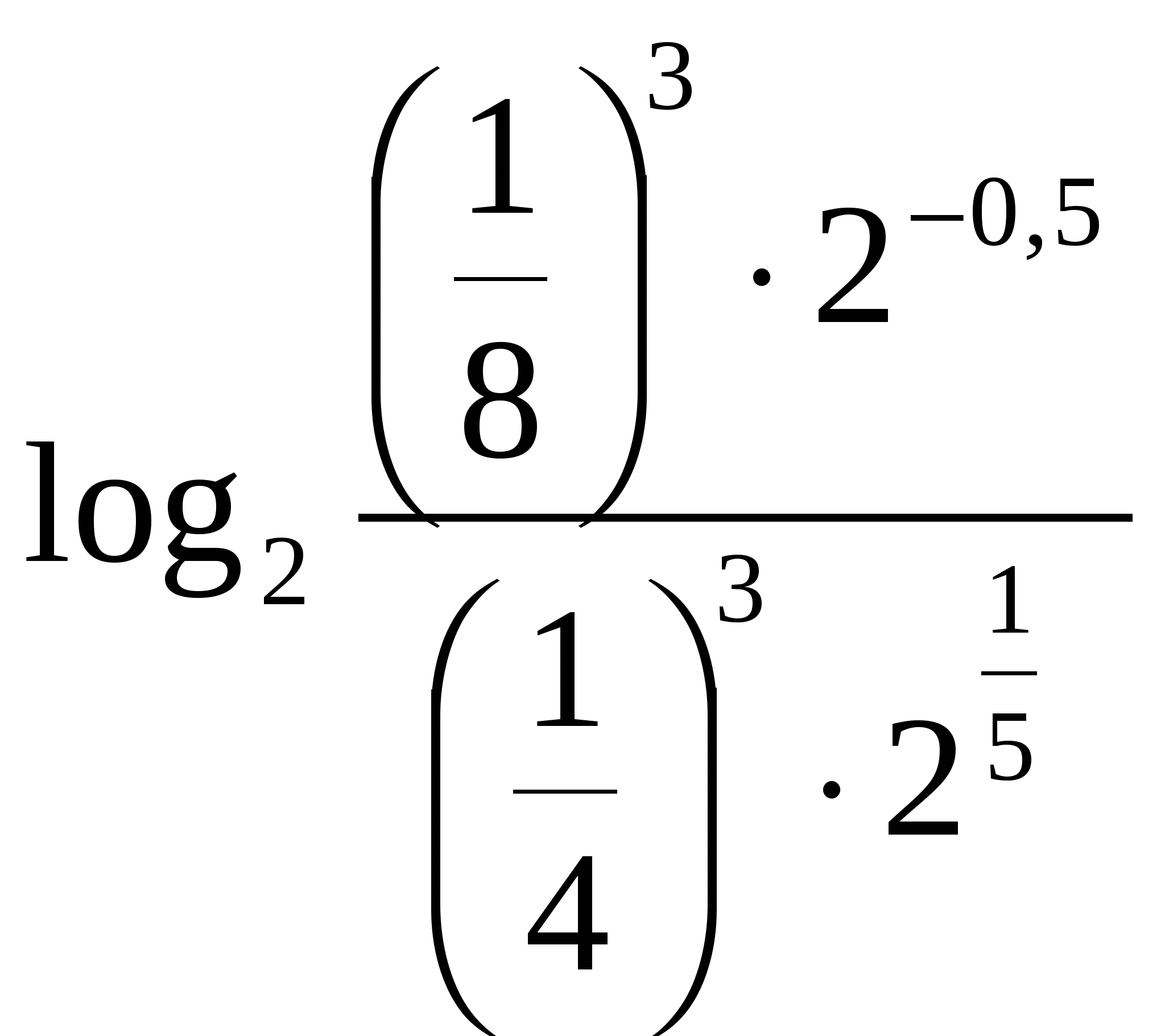 . .5. Сравните числа: а) ___________________________________________________________ 6. Решите неравенство ______________________________________ 7. Решите неравенство Вариант 2 1. Постройте график функции: а) 2. Решите уравнение: а) 3. Решите неравенство 4. Вычислите 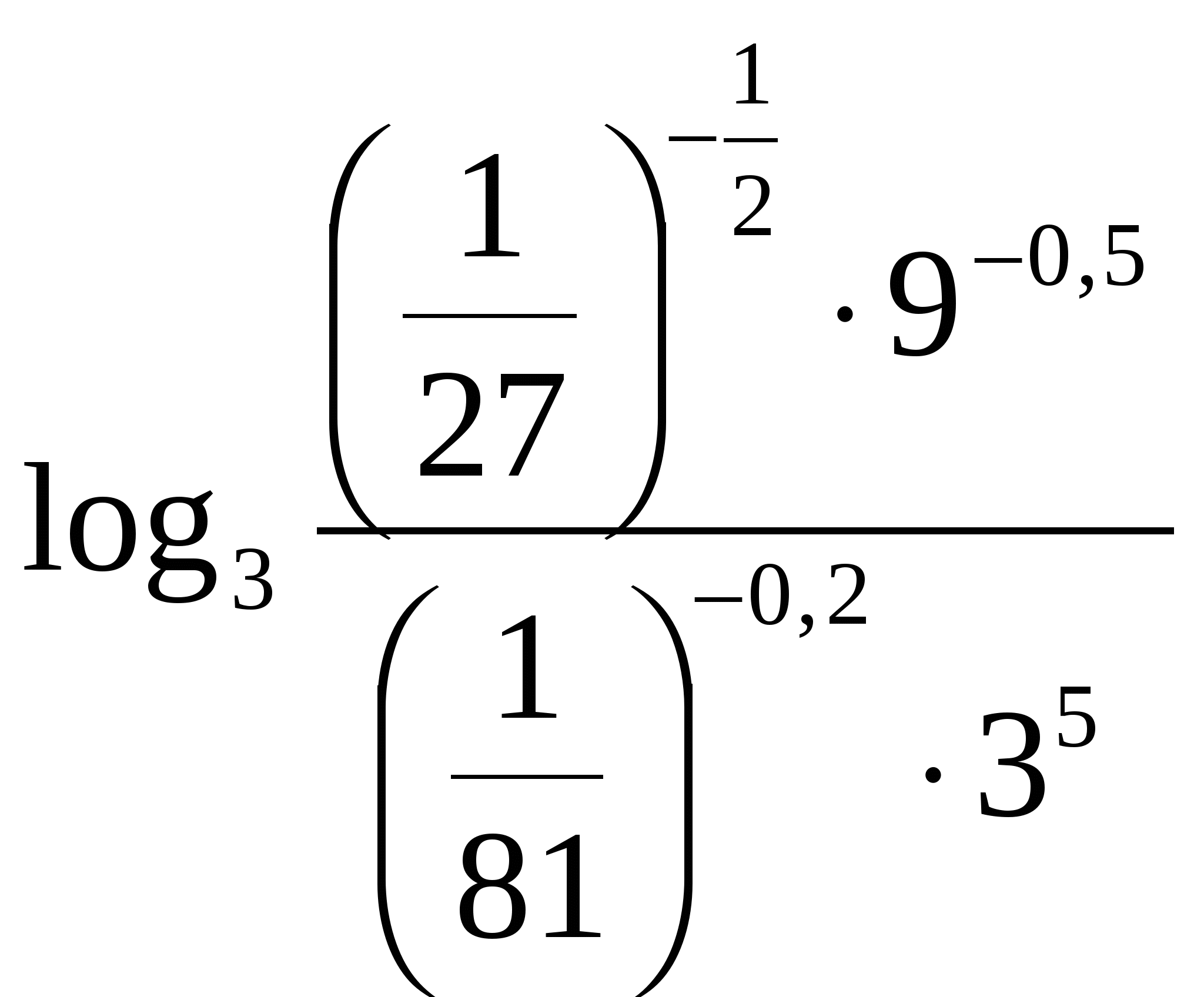 . .5. Сравните числа: а) 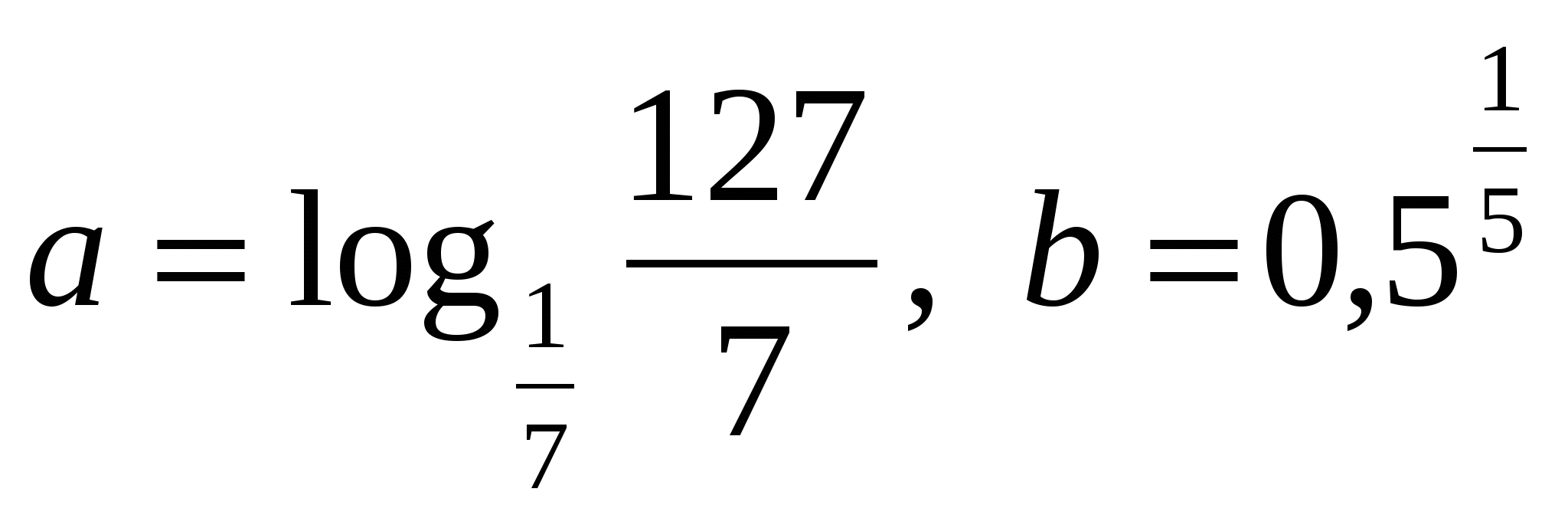 ; б) ; б) ___________________________________________________________ 6. Решите неравенство ______________________________________
Контрольная работа № 5 (2 ч) Вариант 1 1. Вычислите
а) б) в)
а) 4. Исследуйте функцию 5. К графику функции ___________________________________________________________ 6. Решите неравенство ___________________________________ 7. Решите систему уравнений 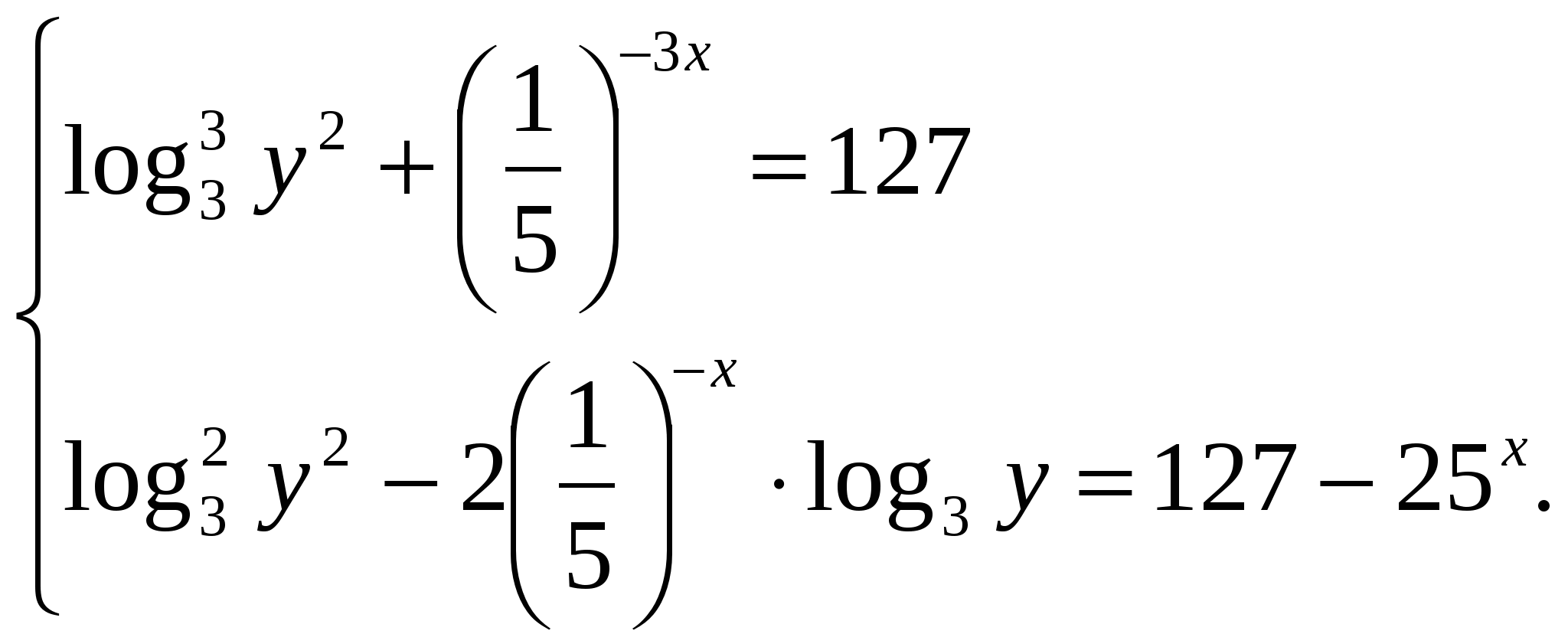 Вариант 2 1. Вычислите 2. Решите уравнение: а) б) в) 3. Решите неравенство: а) 4. Исследуйте функцию 5. К графику функции ___________________________________________________________ 6. Решите неравенство ___________________________________ 7. Решите систему уравнений 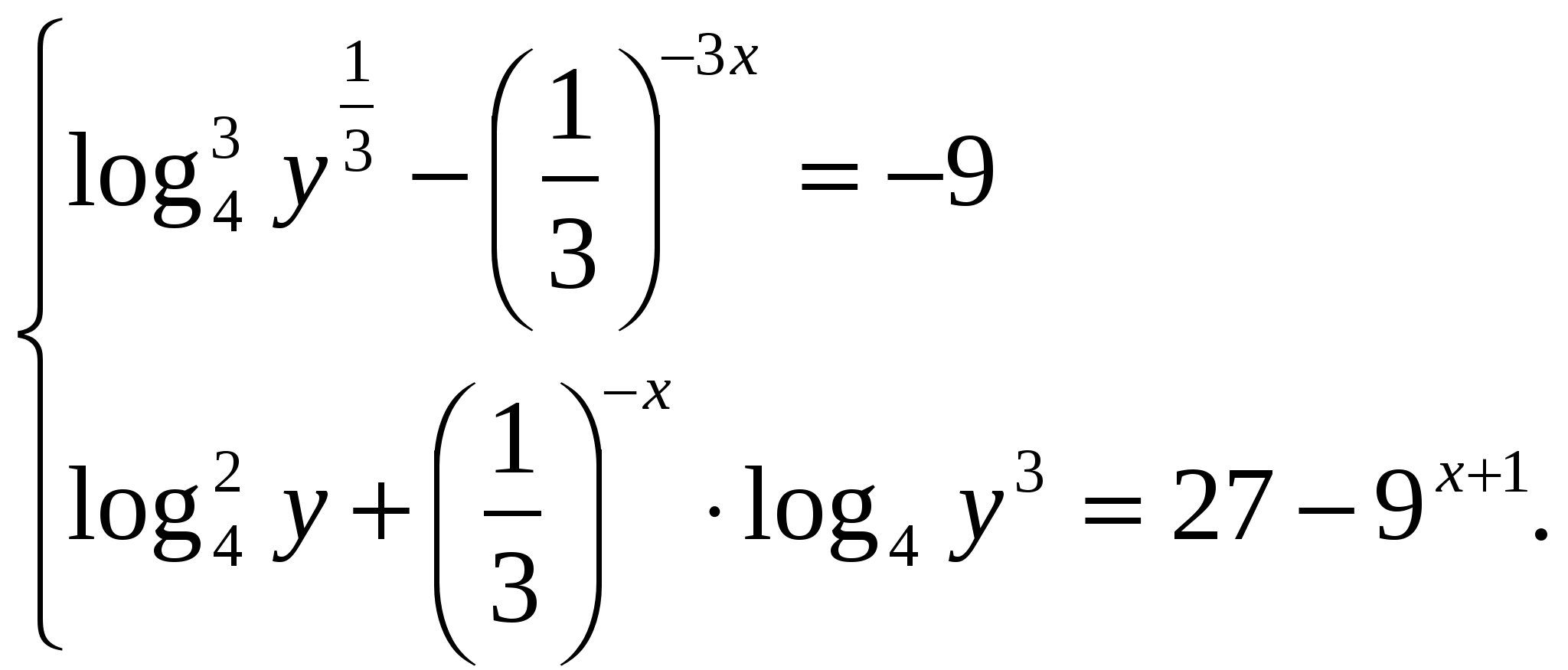 Контрольная работа № 6 (1 ч) Вариант 1 1. Докажите, что функция функции 2. Для данной функции которой проходит через точку 3. Вычислите определенный интеграл: а) 4. Найдите площадь фигуры, ограниченной графиком функции __________________________________________________________ 5. Известно, что функция ___________________________________
Вариант 2 1. Докажите, что функция функции 2. Для данной функции 3. Вычислите определенный интеграл: а) 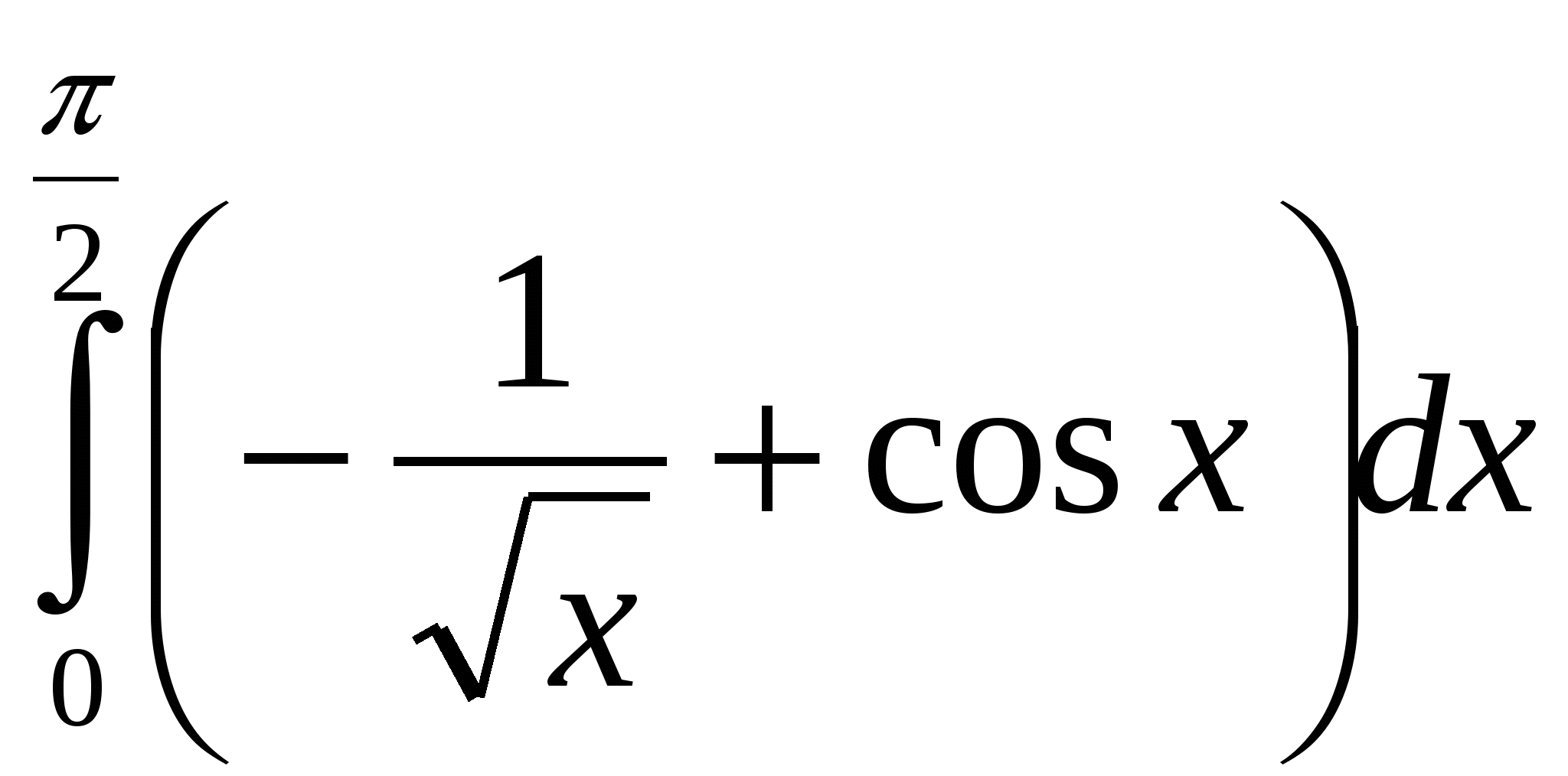 ; б) ; б) 4. Найдите площадь фигуры, ограниченной графиком функции _________________________________________________________ 5. Известно, что функция ___________________________________
Контрольная работа № 7 (2 ч) Вариант 1 1. Решите уравнение: а) б) в)
а)
_________________________________________________________
___________________________________ 6. Решите уравнение Вариант 2 1. Решите уравнение: а) б) в) 2. Решите неравенство: а) 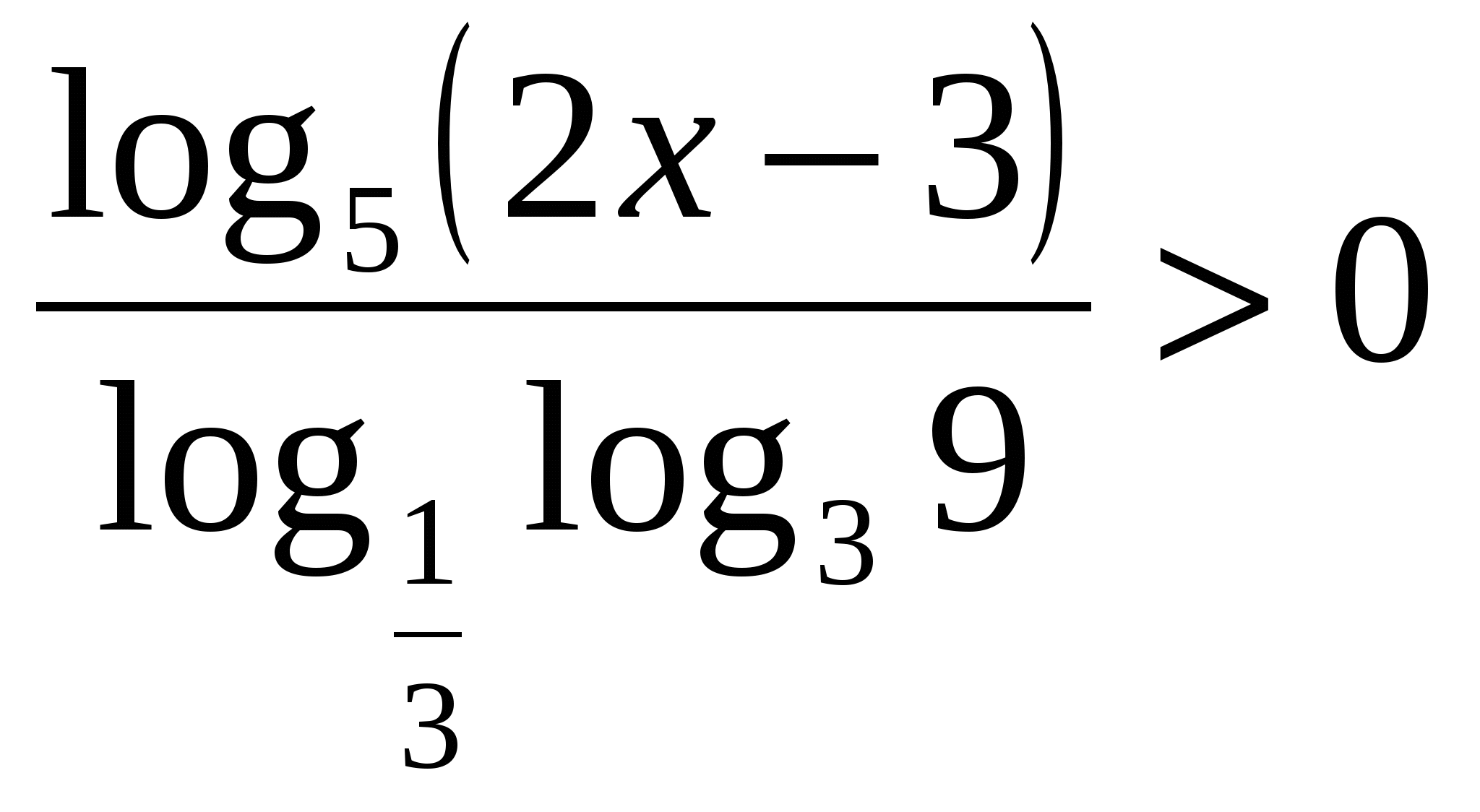 ; б) ; б) 3. Решите уравнение 4. Решите уравнение _________________________________________________________ 5. Внутри квадрата случайным образом выбрана точка. Какова вероятность того, что она расположена внутри вписанного в него круга? _________________________________ 6. Решите уравнение Контрольная работа № 8 (2 ч) Вариант 1 1. Решите уравнение: а)
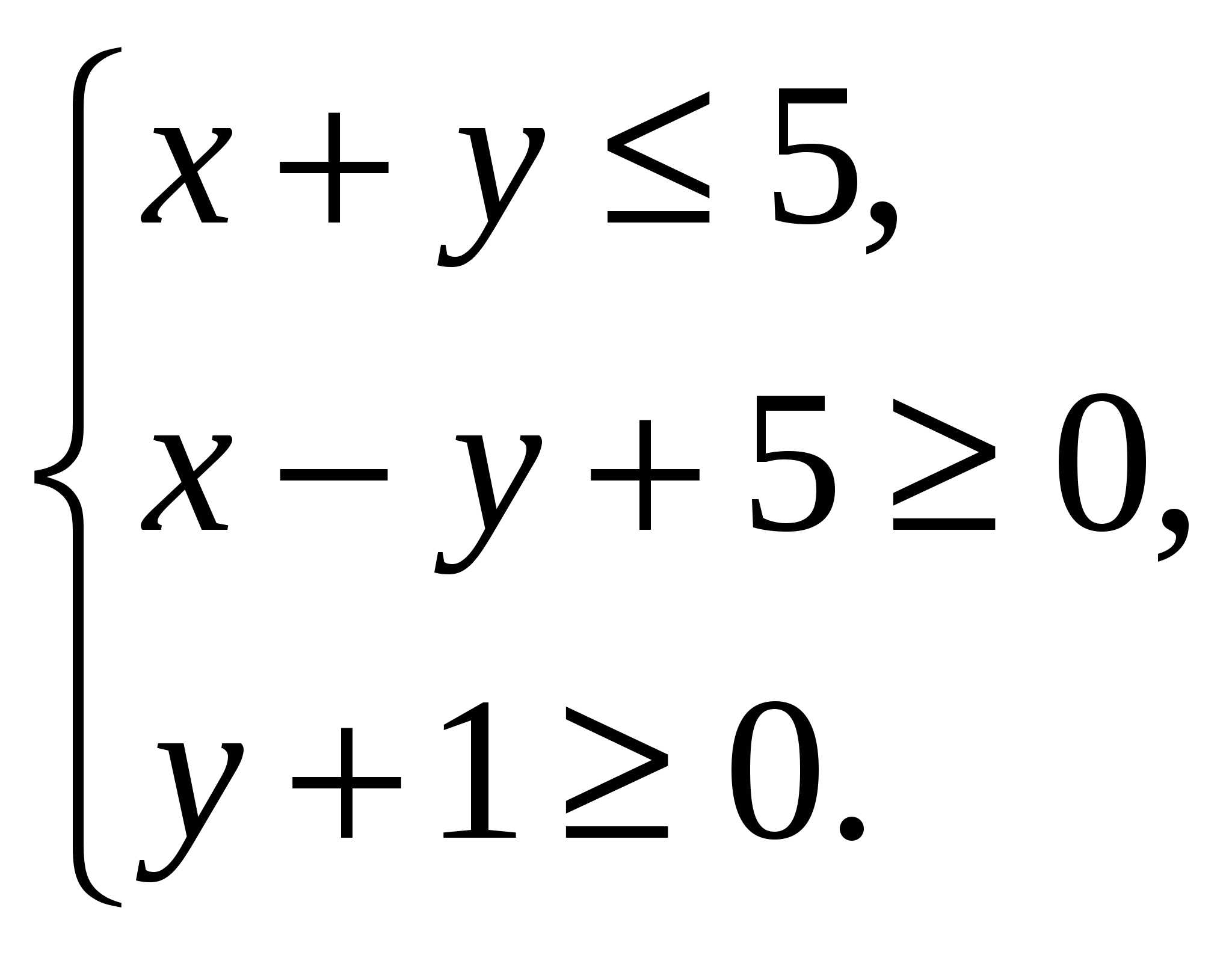 5. Докажите, что для любых неотрицательных чисел ___________________________________________________________ 6. Решите уравнение в целых числах: ________________________________ 7. Три числа образуют арифметическую прогрессию. Если третий член данной прогрессии уменьшить на 3, то полученные три числа составят геометрическую прогрессию. Если второй член геометрической прогрессии уменьшить на Вариант 2 1. Решите уравнение: а) 2. Решите неравенство 3. Решите систему уравнений: а) 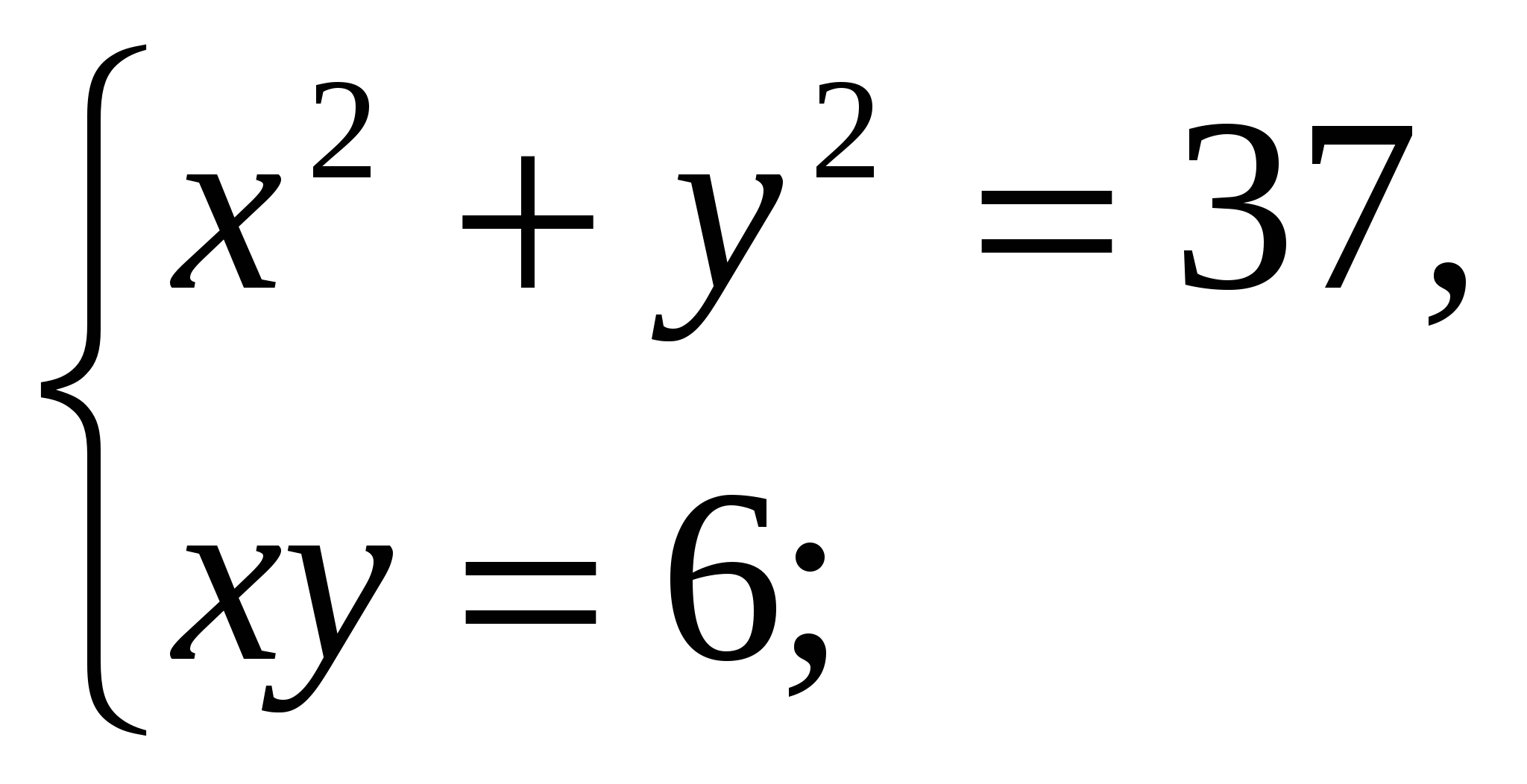 б) б)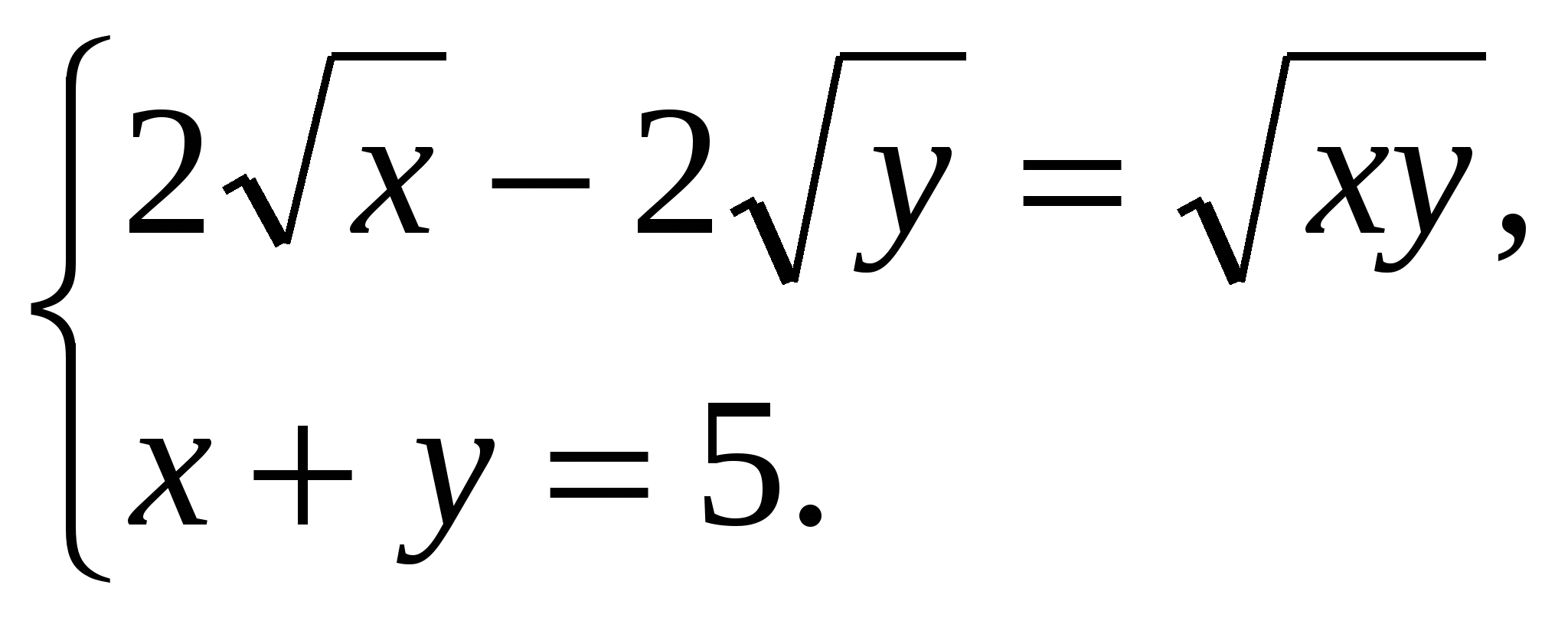 4. Найдите площадь фигуры, заданной системой неравенств 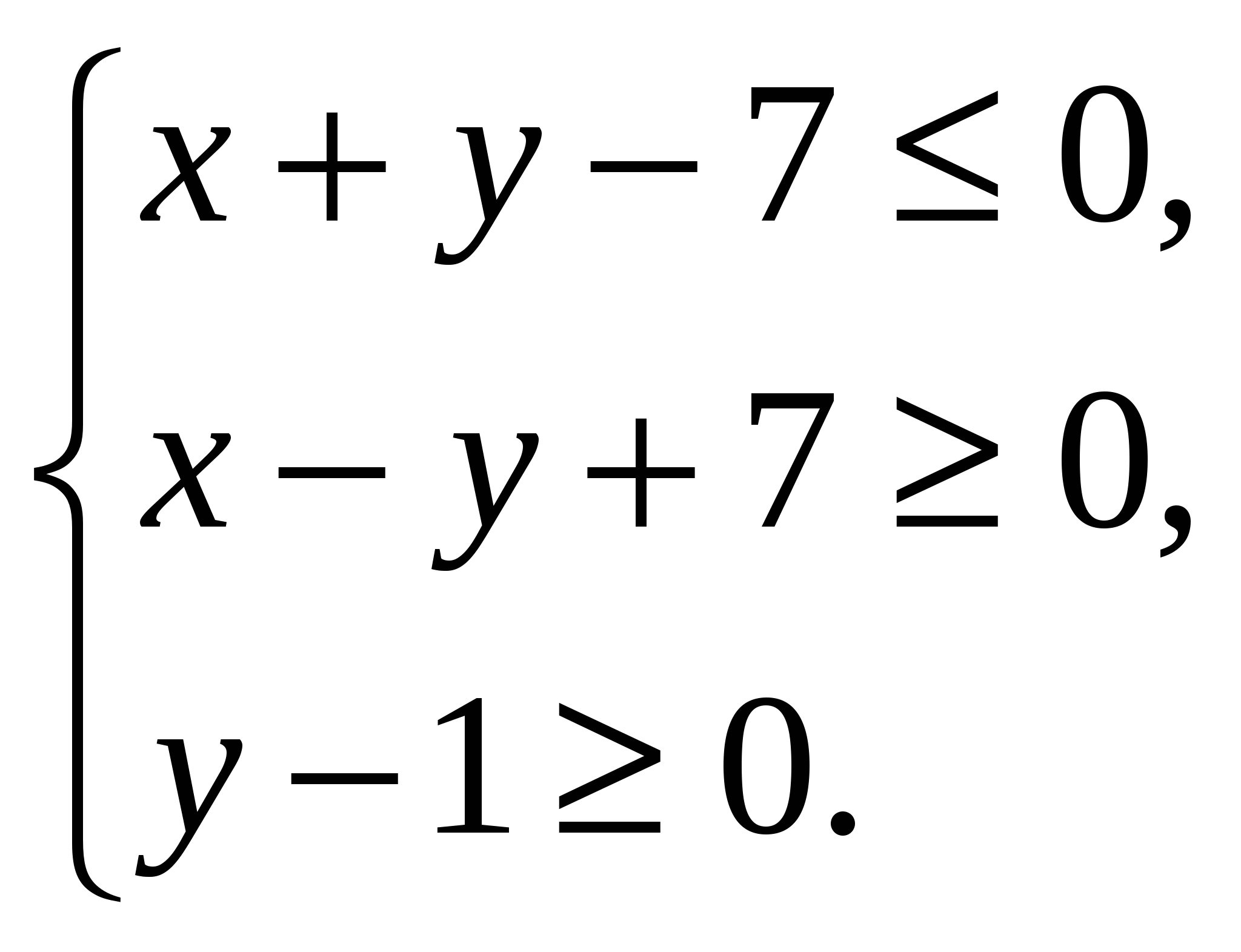 5. Докажите, что для любых неотрицательных чисел выполняется неравенство ___________________________________________________________ 6. Решите уравнение в целых числах: ___________________________________ 7. Три числа составляют геометрическую прогрессию. Если второй член данной прогрессии увеличить на 2, то полученные числа составят арифметическую прогрессию. Если третий член новой прогрессии увеличить на 9, то полученные три числа составят геометрическую прогрессию. Найдите первоначально заданные числа. КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ Контрольная работа № 5.1 Метод координат в пространстве Вариант 1 1. Вычислите скалярное произведение векторов 2. Дан куб АBCDA1B1C1D1. Найдите угол между прямыми AD1 и ВМ, где М – середина ребра DD1. 3. При движении прямая а отображается на прямую а1, а плоскость α – на плоскость α1. Докажите, что если а║α, то а1║ α1. Вариант 2 1. Вычислите скалярное произведение векторов 2. Дан куб АBCDA1B1C1D1. Найдите угол между прямыми AС и DС1. 3. При движении прямая а отображается на прямую а1, а плоскость α – на плоскость α1. Докажите, что если а┴α, то а1┴ α1. Контрольная работа № 6.1 Цилиндр, конус, шар. Вариант 1 1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь полной поверхности цилиндра. 2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 1200. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 300 б) площадь боковой поверхности конуса. 3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45о к нему. Найдите длину линии пересечения сферы этой плоскостью. Вариант 2 1. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найдите площадь полной поверхности цилиндра. 2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 300. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 600 б) площадь боковой поверхности конуса. 3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30о к нему. Найдите площадь сечения шара этой плоскостью. Контрольная работа № 7.1 Объёмы тел Вариант 1 1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60о. Найдите отношение объёмов конуса и шара. 2. Объём цилиндра равен 96π см3, площадь его осевого сечения – 48 см2. Найдите площадь сферы, описанной около цилиндра. Вариант 2 1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса. 2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра. Лист внесения изменений и дополнений
|
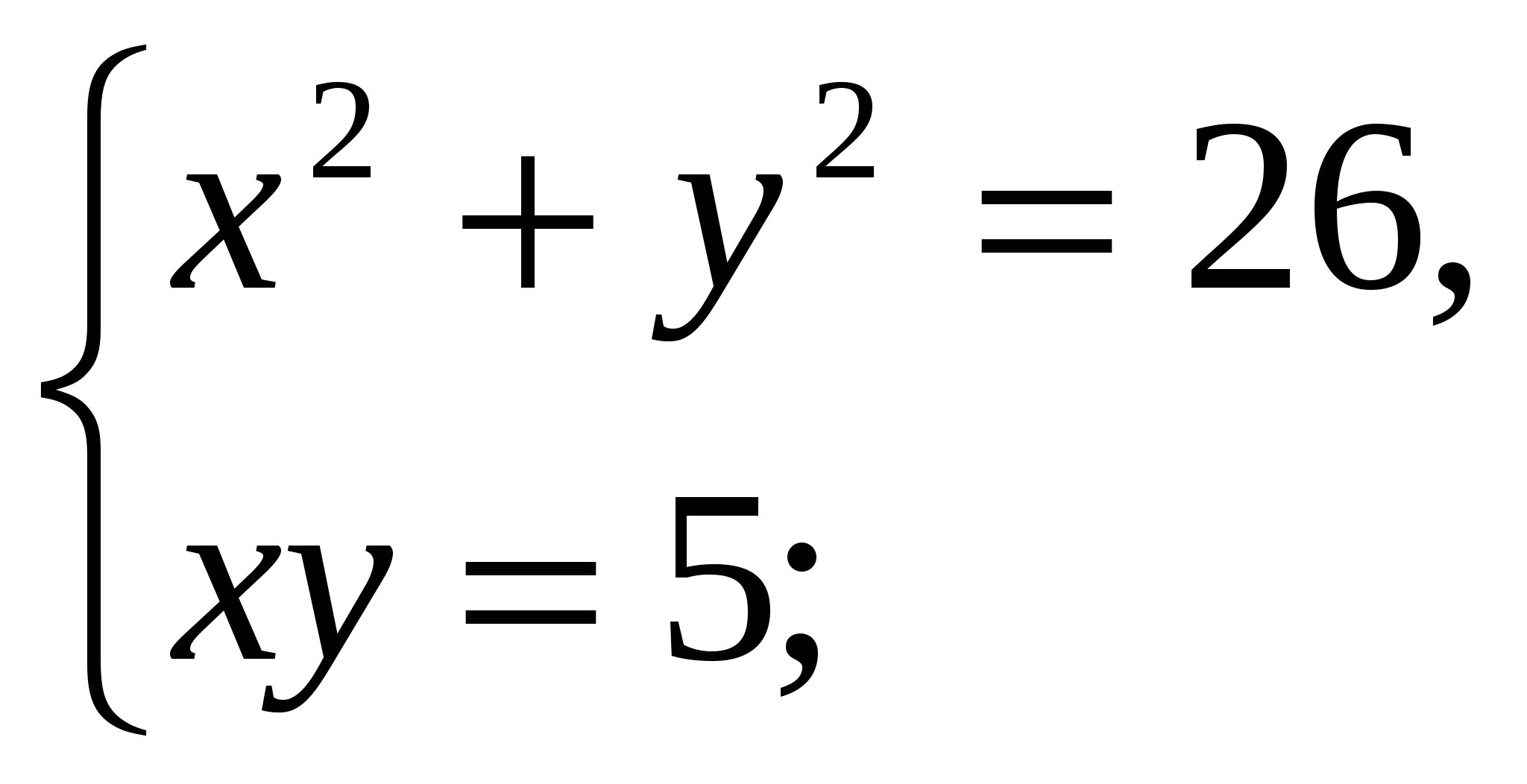 б)
б)