Протокол № от 2012г. «Согласовано» Заместитель директора мбоу сош №3 /./. 2012г

Числовые и буквенные выражения

• 
  выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
  
• 
  применять понятия, связанные с делимостью целых чисел, при решении математических задач;
  
• 
  находить корни многочленов с одной переменной, раскладывать многочлены на множители;
  
• 
  выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
  
• 
  проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
  

• 
  практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
  

Функции и графики

• 
  определять значение функции по значению аргумента при различных способах задания функции;
  
• 
  строить графики изученных функций, выполнять преобразования графиков;
  
• 
  описывать по графику и по формуле поведение и свойства функций;
  
• 
  решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
  

• 
  описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
  

Начала математического анализа

• 
  находить сумму бесконечно убывающей геометрической прогрессии;
  
• 
  вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
  
• 
  исследовать функции и строить их графики с помощью производной,;
  
• 
  решать задачи с применением уравнения касательной к графику функции;
  
• 
  решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
  
• 
  вычислять площадь криволинейной трапеции;
  

• 
  решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
  

Уравнения и неравенства

• 
  решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
  
• 
  доказывать несложные неравенства;
  
• 
  решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
  
• 
  изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
  

• 
  решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
  

• 
  построения и исследования простейших математических моделей.
  

• 
  решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
  
• 
  вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
  

• 
  анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
  

• 
  соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
  
• 
  изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
  
• 
  решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
  
• 
  проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
  
• 
  вычислять линейные элементы и углы в пространственных конфигурациях, площади поверхностей, изученных многогранников;
  
• 
  применять координатно-векторный метод для вычисления отношений, расстояний и углов;
  
• 
  строить сечения многогранников и изображать сечения тел вращения.
  

• 
  исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
  
• 
  вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
  

№ п/п	Наименование разделов и тем	Кол-во часов		Форма контроля	Дата
					План 11бв		Факт 11бв
	Повторение материала 10 класса	4
1	Тригонометрические функции, их свойства и графики	1
2	Решение тригонометрических уравнений	1
3	Производная и её применение для исследования функции	1
4	Производная, её применение для нахождения наибольшего (наименьшего) значения функции	1
	Глава 1.Многочлены	10
5-7	§1 Многочлены от одной переменной	3		ср
8-10	§2 Многочлены от нескольких переменных	3
11-13	§3 Уравнения высших степеней	3		ср
14	Контрольная работа №1 «Многочлены»	1		кр
	Глава 2. Степени и корни. Степенные функции.	24
15-16	§4 Понятие корня n-й степени из действительно числа	2
17-19	§5 Функции y =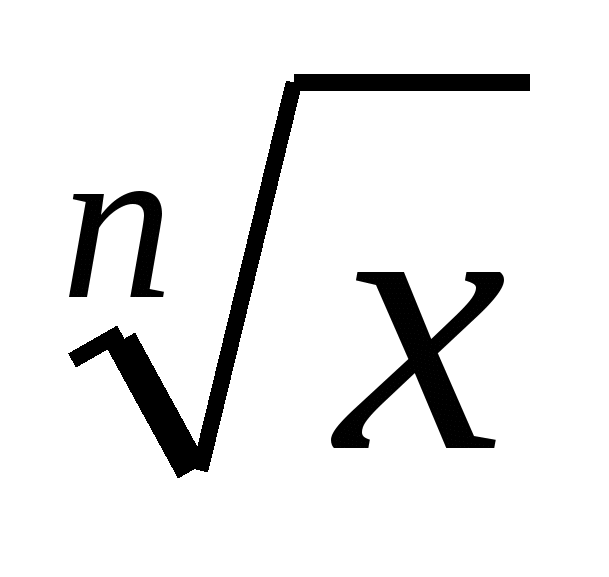, их свойства и графики	3
20-22	§6 Свойства корня n-й степени	3		ср
23-26	§7 Преобразование выражений, содержащих радикалы	4
27-28	Контрольная работа №2 «Степени и корни»	2		кр
29-31	§8 Понятие степени с любым рациональным показателем	3
32-35	§9 Степенные функции, их свойства и графики	4		ср
36-37	§10 Извлечение корней из комплексных чисел	2
38	Контрольная работа №3 «Степенные функции»	1		кр
	Глава 3. Показательная и логарифмическая функции	31
39-41	§11 Показательная функция, ее свойства и график	3
42-44	§12 Показательные уравнения	3		ср
45-46	§13 Показательные неравенства	2
47-48	§14 Понятие логарифма	2
49-51	§15 Логарифмическая функция, ее свойства и график	3
52-53	Контрольная работа №4 «Показательная и логарифмическая функции»	2		кр
54-57	§ 16 Свойства логарифмов	4
58-61	§17 Логарифмические уравнения	4		ср
62-64	§18 Логарифмические неравенства	3		ср
65-67	§19 Дифференцирование показательной и логарифмической функций	3
68-69	Контрольная работа №5 «Логарифмические уравнения и неравенства»	2		кр
	Глава 4. Первообразная и интеграл	9
70-72	§20 Первообразная и неопределенный интеграл	3
73-77	§21 Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона- Лейбница.	2
	Вычисление площадей плоских фигур с помощью определенного интеграла.	3		ср
78	Контрольная работа №6 «Первообразная и интеграл»	1		кр
	Глава 5. Элементы теории вероятностей и математической статистики	9
79-80	§22 Вероятность и геометрия	2
81-83	§23 Независимые повторения испытаний с двумя исходами	3		ср
84-85	§24 Статистические методы обработки информации	2
86-87	§25 Гауссова кривая. Закон больших чисел	2
	Глава 6. Уравнения и неравенства. Системы уравнений и неравенств	33
88-91	§26 Равносильность уравнений	4
92-94	§27 Общие методы решения уравнений	3		ср
95-97	§28 Равносильность неравенств	3
98-100	§29 Уравнения и неравенства с модулями	3
101-102	Контрольная работа №7 «Уравнения и неравенства»	2		кр
103-105	§30 Уравнения и неравенства со знаком радикала	3		ср
106-107	§31 Уравнения и неравенства с двумя переменными	2
108-110	§32 Доказательство неравенств	3
111-114	§33 Системы уравнений	4		ср
115-116	Контрольная работа №8 «Системы уравнений и неравенств »	2		кр
117-120	§34 Уравнения с параметрами	2
	Неравенства с параметрами	2
	Обобщающее повторение	20
121-122	Повторение. «Степени и корни. Степенная функция»	2		тест
123-124	Повторение. «Показательная и логарифмическая функции»	2		тест
125-126	Повторение. «Первообразная и интеграл»	2
127-128	Повторение. «Элементы математической статистики, комбинаторики и теории вероятности»	2		тест
129-130	Повторение. «Уравнения и неравенства. Системы уравнений и неравенств»	2
131-140	Учебно-тренировочные тестовые задания ЕГЭ	10		тест
	итого	140
ГЕОМЕТРИЯ
	Глава IV. Векторы в пространстве	6
1	§1. Понятие вектора в пространстве	1
2-3	§2.Сложение и вычитание векторов. Умножение вектора на число	2
4-5	§3. Компланарные векторы	2
6	Зачет №1 «Векторы в пространстве»	1	зачет
	Глава V. Метод координат в пространстве. Движения.	15
7-12	§1. Координаты точки и координаты вектора	2
	Связь между координатами векторов и координатами точек	2	ср
	Простейшие задачи в координатах	2
13-17	§ 2. Скалярное произведение векторов	3	ср
	Уравнение плоскости	2
18-19	§3 Движения	2
20	Контрольная работа №5.1 «Метод координат в пространстве»	1	кр
21	Зачет №2 «Метод координат в пространстве»	1	зачет
	Глава VI Цилиндр, конус и шар	16
22-24	§ 1. Цилиндр. Площадь поверхности цилиндра	3	ср
25-28	§ 2. Конус. Площадь поверхности конуса.	3	ср
	Усеченный конус.	1
29-35	§ 3. Сфера и шар. Уравнение сферы.	3
	Взаимное расположение сферы и плоскости. Касательная плоскость к сфере.	3	ср
	Площадь сферы.	1
36	Контрольная работа № 6.1«Цилиндр, конус и шар»	1	кр
37	Зачет №3 «Цилиндр, конус и шар»	1	зачет
	Глава VII. Объемы тел	17
38-40	§ 1. Объем прямоугольного параллелепипеда	3	ср
41-42	§ 2. Объем прямой призмы и цилиндра	2
43-47	§ 3. Объем наклонной призмы, пирамиды и конуса	1	ср
	Объем пирамиды.	2
	Объем конуса.	2
48-52	§ 4. Объем шара и площадь сферы	3	ср
	Объем шарового сегмента, шарового слоя и шарового сектора.	2
53	Контрольная работа №7.1 «Объемы тел»	1	кр
54	Зачет №4 «Объемы тел»	1	зачет
	Заключительное повторение при подготовке к итоговой аттестации по геометрии	16
55	Аксиомы стереометрии и их следствия. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей.	1
56	Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью.	1
57	Двугранный угол. Перпендикулярность плоскостей.	1
58	Многогранники: параллелепипед, призма, пирамида, площади их поверхностей.	1
59	Векторы в пространстве. Действия над векторами. Скалярное произведение векторов.	1
60	Цилиндр, конус и шар, площади их поверхностей.	1
61	Объемы тел.	1
62-70	Учебно-тренировочные тестовые задания ЕГЭ	9	тест
	итого	70
	ИТОГО	210