Рабочая программа составлена на основе

Название	Рабочая программа составлена на основе
Дата	11.04.2016
Размер	164.09 Kb.
Тип	Рабочая программа

Пояснительная записка
Рабочая программа составлена на основе

1. Сборник нормативных документов, Математика/Сост. Э.Д. Днепров, М:Дрофа,2004
2. Программы. Математика 5-6 классы, алгебра 7-9 кл, алгебра и начала математического анализа 10-11 классы. Авт.-сост. И.И. Зубарева, А.Г. Мордкович. Мнемозина, 2011.

3 .Программы общеобразовательных учреждений . Геометрия ,10-11 классы. Москва. Просвещение, 2010. Бурмистрова Т.А.
Учебники :

1.Алгебра и начала анализа : задачник. для 10-11 кл. общеобразоват. учреждений/ А.Г. Мордкович – М .: Мнемозина 2010

2.Алгебра и начала анализа : учеб. для 10-11 кл. общеобразоват. учреждений/ А.Г.Мордкович – М .: Мнемозина 2010

Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации в 11 классе на изучение математики отводится 5 часов в неделю или 170 часов в год.

Цели:

Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:

 формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

 развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;

 овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;

 воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.

Тематическое планирование курса алгебры - 10 класс, общеобразовательный уровень

№ п/п	Содержание учебного материала	Количество часов по рабочей программе
1	Повторение основного курса средней школы и 10 класса	6
2	Степени и корни. Степенные функции	12
3	Показательная и логарифмическая функции	25
4	Первообразная и интеграл	8
5	Элементы комбинаторики, статистики и теории вероятностей	11
6	Тренировочные тематические задания	8+8
7	Уравнения и неравенства. Системы уравнений и неравенств	18
8	Итоговое повторение.	6
итого		102

ОСНОВНОЕ СОДЕРЖАНИЕ

АЛГЕБРА

Повторение основного курса средней школы и 10 класса (6 часов)

Степени и корни. Степенные функции (12 часов).

Понятие корня n-ой степени из действительного числа. Функции y =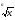

, их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.

Степенные функции, их свойства и графики.
Показательная и логарифмическая функции (25 часа)

Показательная функция, её свойства и график. Показательные уравнения.

Показательные неравенства. Понятие логарифма. Логарифмическая функция, её свойства и график. Свойства логарифма. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования. Логарифмические уравнения.

Логарифмические неравенства. Дифференцирование показательной и логарифмической функций.
Первообразная и интеграл (8 часов).

Первообразная и неопределенный интеграл. Понятие об определенном интеграле как площади криволинейной трапеции. Формула Ньютона-Лейбница

Элементы комбинаторики, статистики и теории вероятностей (11 часов).

Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.

Уравнения и неравенства. Системы уравнений и неравенств (18 часов)

Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.

Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.

Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.

Тематическое планирование курса геометрии - 10 класс, общеобразовательный уровень

№ п/п	Содержание учебного материала	Количество часов по рабочей программе
1	Метод координат в пространстве	15
2	Цилиндр, конус и шар	17
3	Объемы тел	22
4	Повторение	14
итого		68ч.

ГЕОМЕТРИЯ

Метод координат в пространстве (15 часов)

Прямоугольная система координат в пространстве. Координаты вектора. Угол между векторами. Скалярное произведение векторов. Связь между координатами векторов и координатами точек. Простейшие задачи в координатах. Вычисление углов между прямыми и плоскостями. Движения. Виды движения.

Цилиндр, конус и шар (17 часов)

Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию.

Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел (22 часов)

Объем прямоугольного параллелепипеда. Объем прямой призмы и цилиндра.

Объем наклонной призмы, пирамиды, конуса. Объем шара и площадь сферы.

Повторение (14часов)

Скалярное произведение векторов. Связь между координатами векторов и координатами точек. Простейшие задачи в координатах. Вычисление углов между прямыми и плоскостями. Цилиндр. Конус. Усечённый конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы. Объем прямоугольного параллелепипеда. Объем прямой призмы и цилиндра.

Объем наклонной призмы, пирамиды, конуса. Объем шара и площадь сферы.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на базовом уровне ученик должен

знать/понимать:

 значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

 значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;

 универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;

 вероятностный характер различных процессов окружающего мира.
Алгебра

Уметь:

 выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;

 проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

 вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики

Уметь:

 определять значение функции по значению аргумента при различных способах задания функции;

 строить графики изученных функций;

 описывать по графику и в простейших случаях по формуле2 поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

 решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа

Уметь:

 вычислять производные и первообразные элементарных функций, используя справочные материалы;

 исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;

 вычислять в простейших случаях площади с использованием первообразной;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства

Уметь:

 решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;

 составлять уравнения и неравенства по условию задачи;

 использовать для приближенного решения уравнений и неравенств графический метод;

 изображать на координатной плоскости множества решений простейших уравнений и их систем;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для построения и исследования простейших математических моделей.
Элементы комбинаторики,

статистики и теории вероятностей

Уметь:

 решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;

 вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для анализа реальных числовых данных, представленных в виде диаграмм, графиков;

 анализа информации статистического характера.
Геометрия

Уметь:

 распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;

 описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;

 анализировать в простейших случаях взаимное расположение объектов в пространстве;

 изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

 строить простейшие сечения куба, призмы, пирамиды;

 решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

 использовать при решении стереометрических задач планиметрические факты и методы;

 проводить доказательные рассуждения в ходе решения задач;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;

 вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

Критерии и нормы оценки знаний, умений и навыков

обучающихся по математике.

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

2.Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.

3.2. К негрубым ошибкам следует отнести:

неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.

Литература

А. Г. Мордкович Алгебра и начала анализа 10–11 классы. Учебник - М.: Мнемозина 2009г.;
А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчиская Алгебра и начала анализа 10–11 классы. Задачник – М: Мнемозина 2009 г.;
А. Г. Мордкович Алгебра и начала анализа 10–11 классы. Пособие для учителей М.: Мнемозина 2008 г.;
В. И. Глизбург Алгебра и начала анализа 11 класс. Контрольные работы. Базовый уровень - М.: Мнемозина 2009 г.;
Л. А. Александрова. Алгебра и начала анализа. Самостоятельные работы - М.: Мнемозина 2009 г.
Шабунин М.И. и др. Алгебра начала анализа: Дидактические материалы для 10 – 11 кл. – М.: Мнемозина, 2000
Денищева Л.О. Корешкова Т.А. Алгебра и начала анализа. 10 –11 класс: Тематические тесты и зачеты для общеобразовательных учреждений. Под ред. А.Г. Мордковича.-

М.: Мнемозина, 2009

Ершов А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.:Илекса, 2009
Студенецкая В.Н., (Авт.-сост). Решение задач по статистике, комбинаторике, теории вероятности Волгоград: Учитель, 2005

Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет – ресурсов:

Министерство образования РФ: https://informika.ru/; https://ed.gov.ru/; https://edu.ru/
Тестирование online: 5 - 11 классы : https://kokch.kts.ru/cdo/
Педагогическая мастерская, уроки в Интернет и многое другое: https://teacher.fio.ru
Новые технологии в образовании: https://edu.secna.ru/main/
Путеводитель «В мире науки» для школьников: https://uic.ssu.samara.ru/~nauka/
Мегаэнциклопедия Кирилла и Мефодия: https://mega.km.ru
сайты «Энциклопедий энциклопедий», например: https://rubricon.ru/; https://encyclopedia.ru/