|
Формы работы
Учитывая характеристики классов, использую в каждом классе следующие формы работы: деятельностные, индивидуальные,
подкрепленные оценкой в 8 «А» и в 8 «В» классах. В остальных классах использую разнообразные формы работы: фронтальную,
индивидуальную, групповую. Использую презентации, тесты, индивидуальные карточки и задания. Использую творческие
задания, выполняемые учащимися для устной работы с классом.
Планируемые результаты обучения
Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:
а) в личностном направлении:
1)Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры ;
2) Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) Представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) Креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) Умение контролировать процесс и результат учебной математической деятельности;
6) Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
б) в метапредметном направлении:
1) Первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
2) Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
3) Умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4) Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) Для иллюстрации, интерпретации, аргументации;
5) Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
6) Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
7) Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
8) Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
9) Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
в) в предметном направлении:
1) Овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
2) Умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) Развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) Овладение символьным языком аматематики, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
6) Овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;
7) Овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
8) Овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
9) Усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
10) Умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
11) Умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
Требования к математической подготовке учащихся 8 класса
В результате изучения алгебры ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Контроль выполнения программы осуществляется с помощью контрольных работ , самостоятельных работ, математических диктантов, тестирования.
Структура тематического плана. В соответствии с вышеизложенным, в структуре тематического плана выделяются следующие колонки: номер урока, наименование раздела программы, темы уроков, количество часов, тип урока, УУД., примечание.
Вывод. Таким образом, составленное тематическое планирование соответствует нормативно- правовому сопровождению образовательного процесса и позволяет в полной мере реализовать цели, задачи курса, способствует развитию детей и формированию общеучебных компетенций.
Учебно-тематическое планирование
Алгебра
№
урока
|
месяц
|
Тема урока
|
Форма урока
|
УУД
|
Примеч.
|
I четверть 27 ч.
Рациональные дроби и их свойства (26 часа).
|
Личностные
|
Предметные
|
Метапредметные
|
|
1.
2.-3
|
Сентябрь
|
Понятие рациональной дроби
Допустимые значения переменных, входящих в дробные выражения
|
Урок-лекция
Уроки закрепления знаний
|
Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры.
Умение контролировать процесс и результат учебной математической деятельности
|
Планировать – определить последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий;
• Вычислять числовое значение буквенного выражения; находить область допустимых значений переменных в выражении.
Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей.
Выполнять действия с алгебраическими дробями. Представлять целое выражение в виде многочлена, дробное выражение в виде отношения многочленов, доказывать тождества.
Представлять целое выражение в виде многочлена, дробное - в виде отношения многочленов
|
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом
|
|
4.
5.
6.
|
Основное свойство дроби.
Сокращение дробей.
Следствие из основного свойства дроби
|
Урок - беседа
Урок совершенствования знаний
Урок закрепления знаний
|
7.
8.
9.
|
Сложение и вычитание дробей с одинаковыми знаменателями.
Сложение и вычитание дробей с противоположными знаменателями
Сложение и вычитание дробей с противоположными знаменателями
|
Урок- беседа
Урок изучения нового материала
Уроки закрепления знаний
|
10
11
12
13
|
Правило сложения и вычитания дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями.
Сложение и вычитание рациональной дроби и целого выражения
Сложение и вычитание рациональной дроби и целого выражения
|
Урок-лекция
Урок совершенствования знаний
Уроки закрепления знаний
|
14
|
Сентябрь
|
Контрольная работа №1 «Сложение и вычитание рациональных дробей».
|
Урок контроля знаний
|
|
|
|
15.
|
Правила умножения рациональных дробей
|
Комбинированный урок
|
Выполнять действия с алгебраическими дробями.
Выполнять действия с алгебраическими дробями.
Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей.
|
16
|
Возведение дроби в степень.
|
Урок- беседа
|
17.
18
|
Октябрь
|
Преобразование дробных выражений, содержащих действия умножения.
Правило деления рациональных дробей
|
Комбинированный урок
Урок- практикум
|
19
20
21
22
|
Октябрь
|
Преобразование рациональных выражений.
Совместные действия с рациональными дробями
Преобразование дробных выражений
Нахождение среднего гармонического ряда положительных чисел
|
Теоретическое исследование
Практикум
Комбинированный урок
Комбинированный урок
|
23
24
25
|
Октябрь
|
Построение графика функция 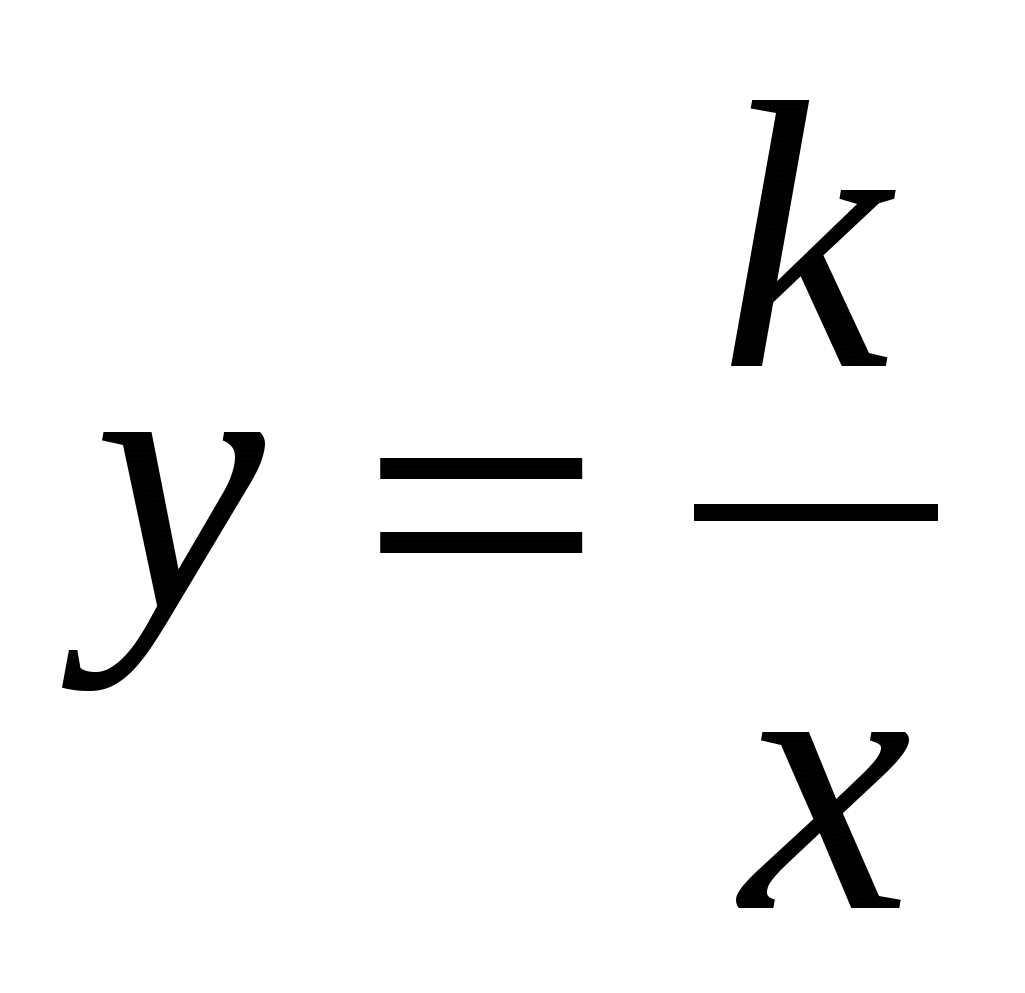
Функция 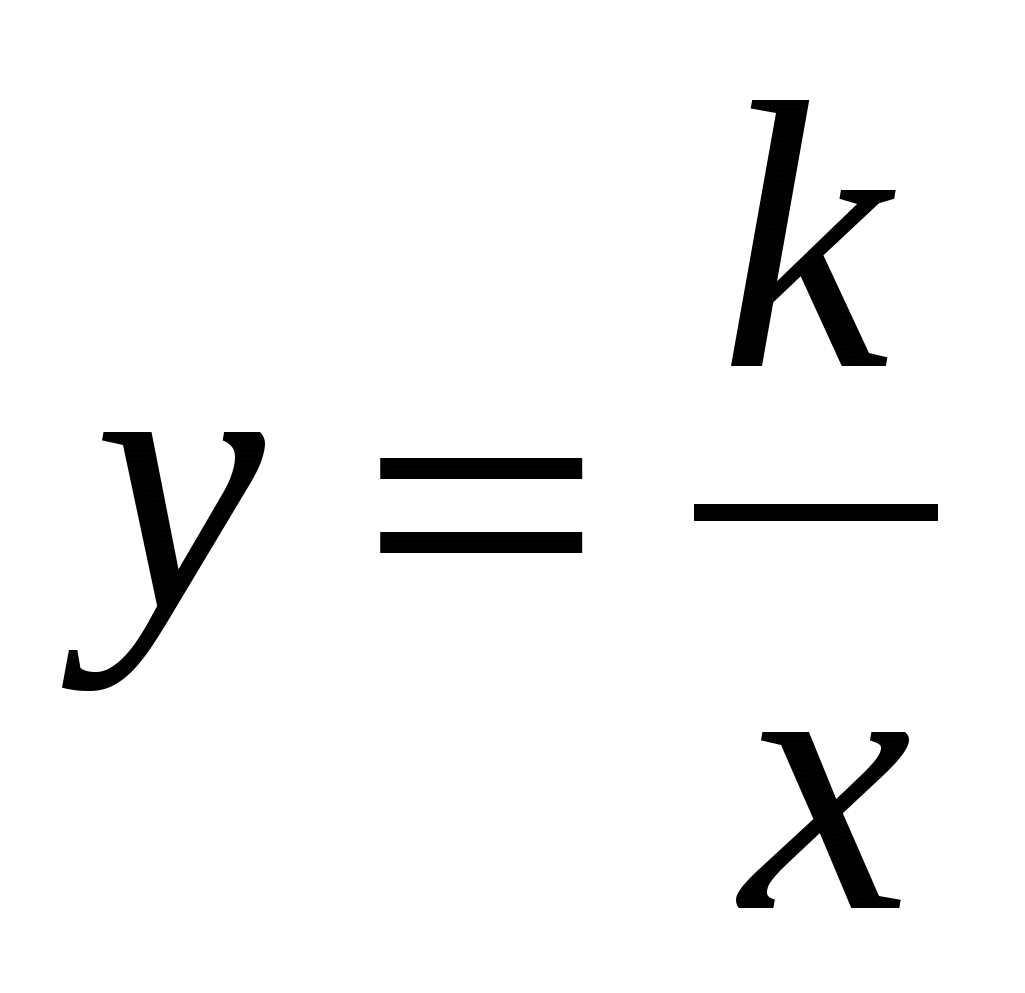 и её график в решении различных задач и её график в решении различных задач
Функция 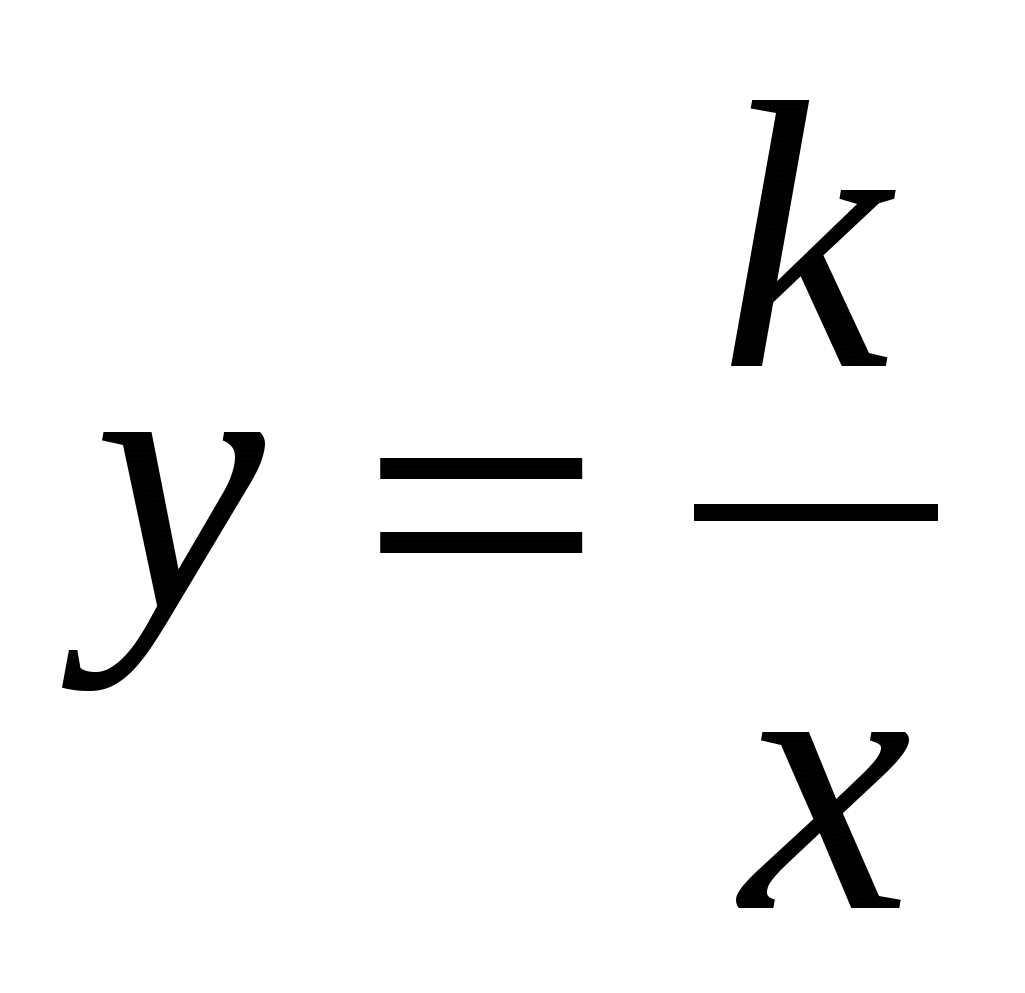 и её график в решении различных задач и её график в решении различных задач
|
Лекция
Решение познавательных задач
Выполнение упражнений
|
Составлять формулы, выражающие зависимости между величинами, вычислять по формулам.
Распознавать прямую и обратную пропорциональные зависимости. Распознавать функцию вида 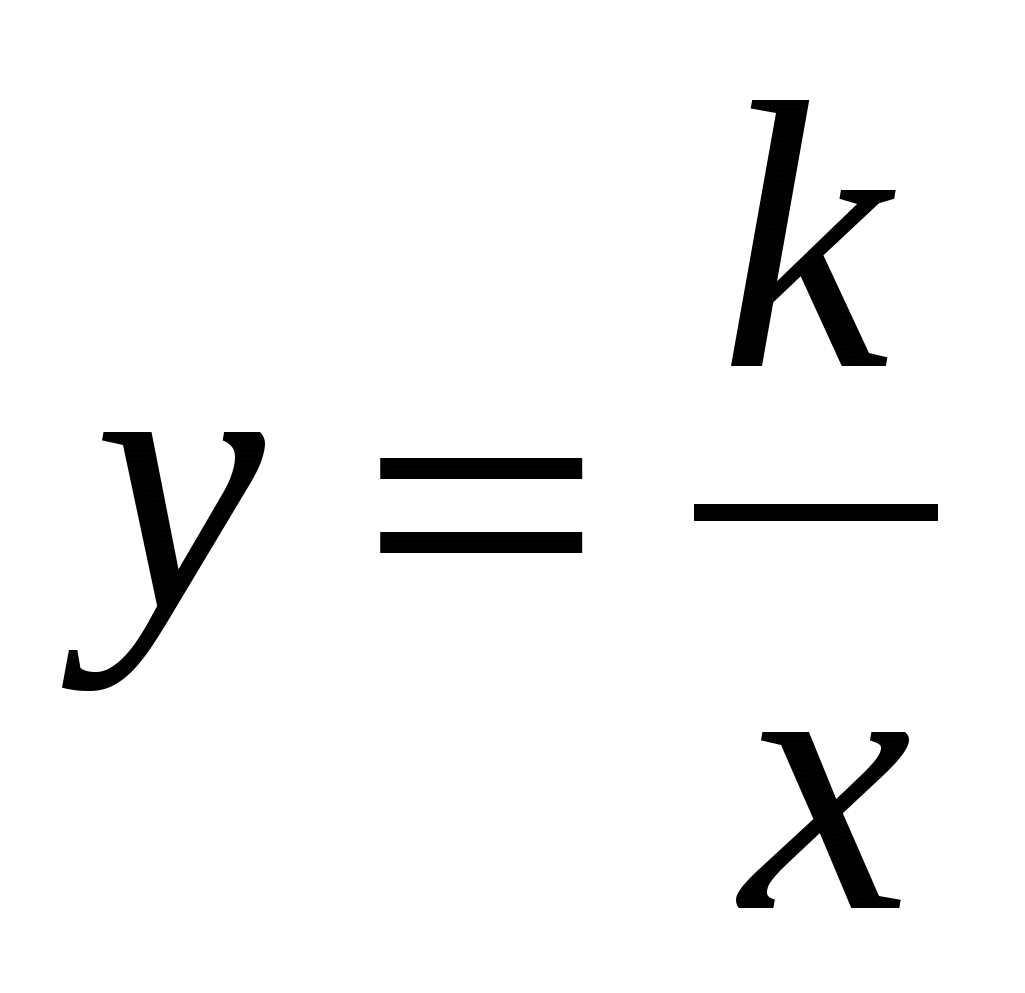 , строить её график, описывать свойства. Показывать схематически положение на координатной плоскости графика функции вида , строить её график, описывать свойства. Показывать схематически положение на координатной плоскости графика функции вида 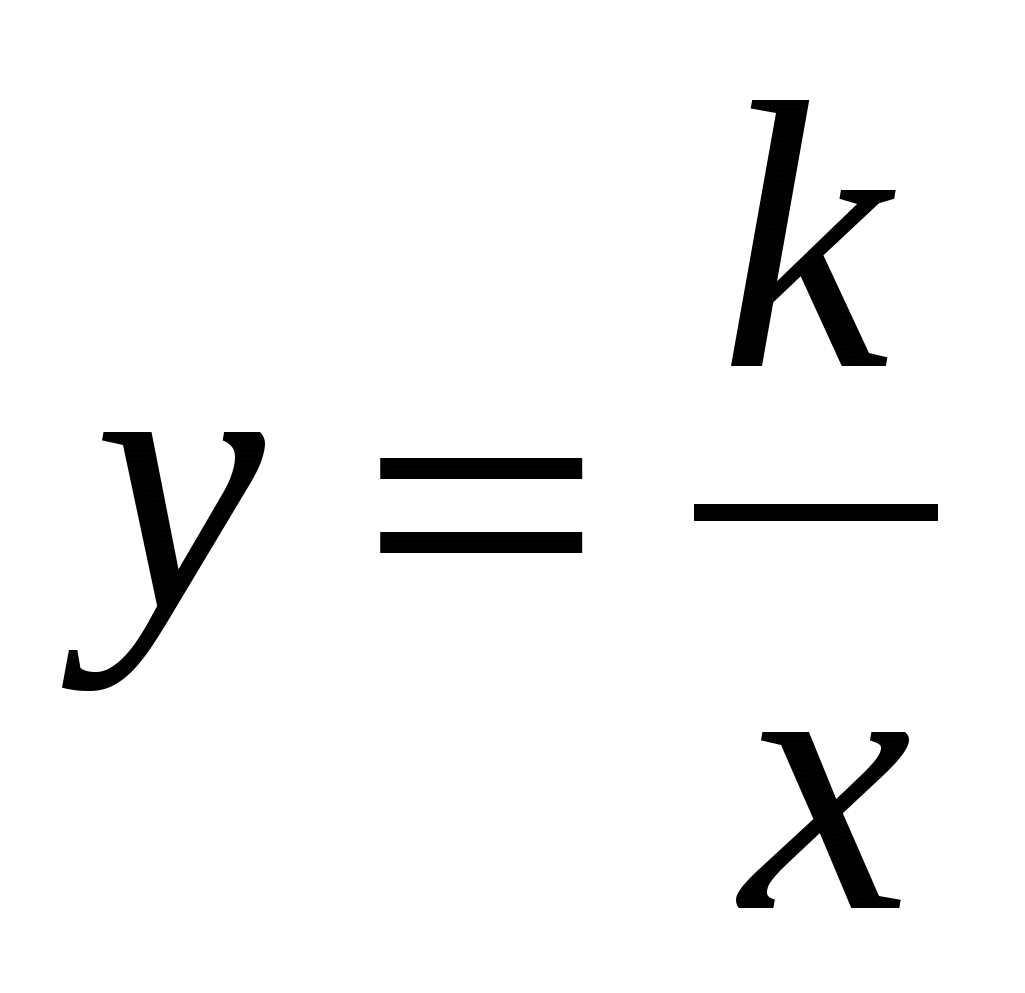 в зависимости от значения коэффициента. в зависимости от значения коэффициента.
|
|
26
|
Октябрь
|
Контрольная работа №2 «Рациональные дроби».
|
Письменная контрольная работа
|
|
|
|
2. Квадратные корни (23 часов)
|
|
26
|
Октябрь
|
Рациональные числа
|
Лекция
|
Представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации
.
Креативность мышления, инициатива, находчивость, активность при решении математических задач.
|
Описывать множество целых чисел, множество рациональных чисел, соотношение между этими множествами.
Приводить примеры иррациональных чисел; распознавать рациональные и иррациональные числа; изображать числа точками на координатной прямой.
Описывать множество действительных чисел.
|
Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.
Умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации.
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом
|
27
28
|
|
Иррациональные числа.
Иррациональные числа.
|
Беседа
Комбинированный урок
|
|
29
30.
31
|
Октябрь
|
Арифметический квадратный корень.
Извлечение квадратного корня
Применение понятия квадратного корня при решении различных задач
|
Лекция
Комбинированный урок
Практикум
|
Формулировать определение квадратного корня из числа. Использовать график функции у = х2 для нахождения квадратных корней.
|
|
|
|
II четверть 21 ч.
|
32
33
|
Октябрь
|
Решение уравнений вида 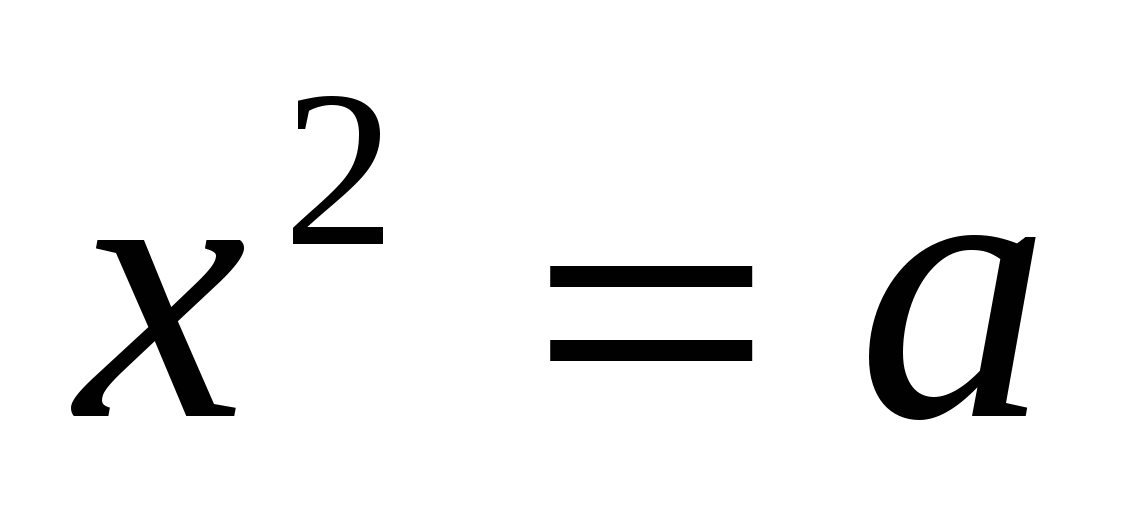 . .
Нахождение приближенного значения квадратного корня.
|
Комбинированный урок
Практикум
|
|
Вычислять точные и приближённые значения квадратных корней, используя при необходимости калькулятор; проводить оценку квадратных корней.
Исследовать уравнение 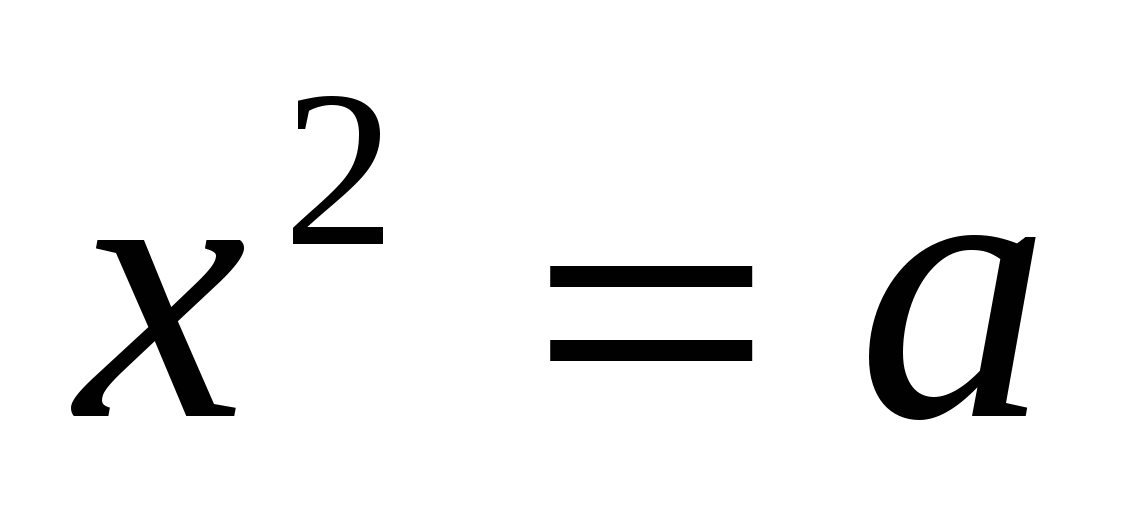 ; находить точные и приближённые корни при а > 0. ; находить точные и приближённые корни при а > 0.
|
34
35
|
Октябрь
Ноябрь
|
Функция 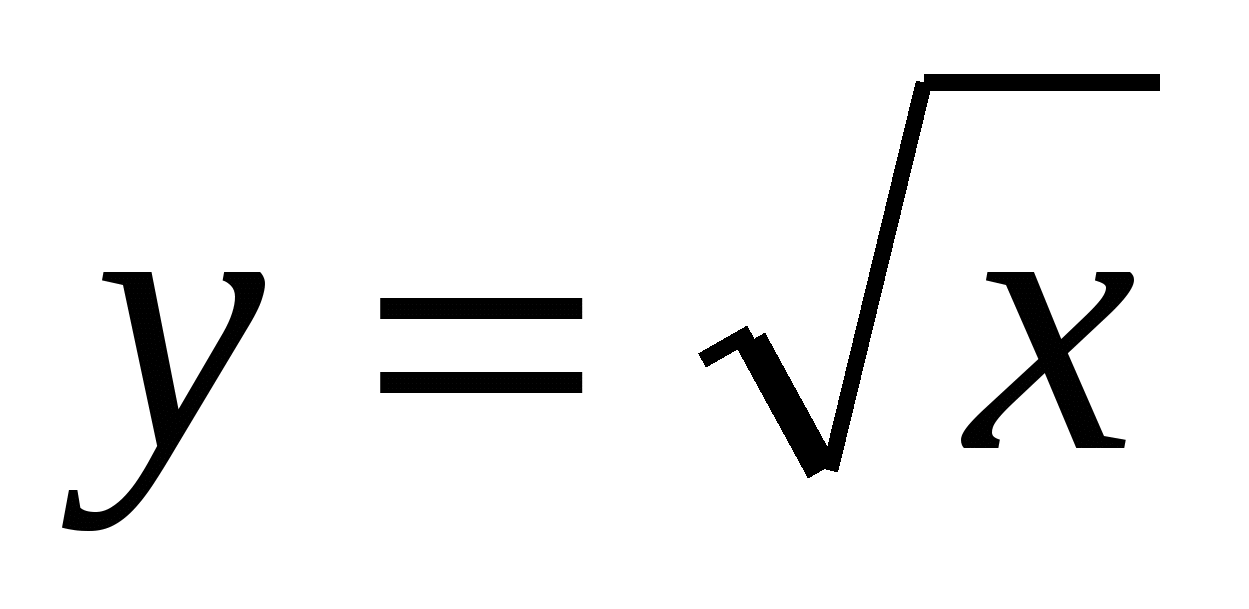 и ее график. и ее график.
Использование графика и свойств функции 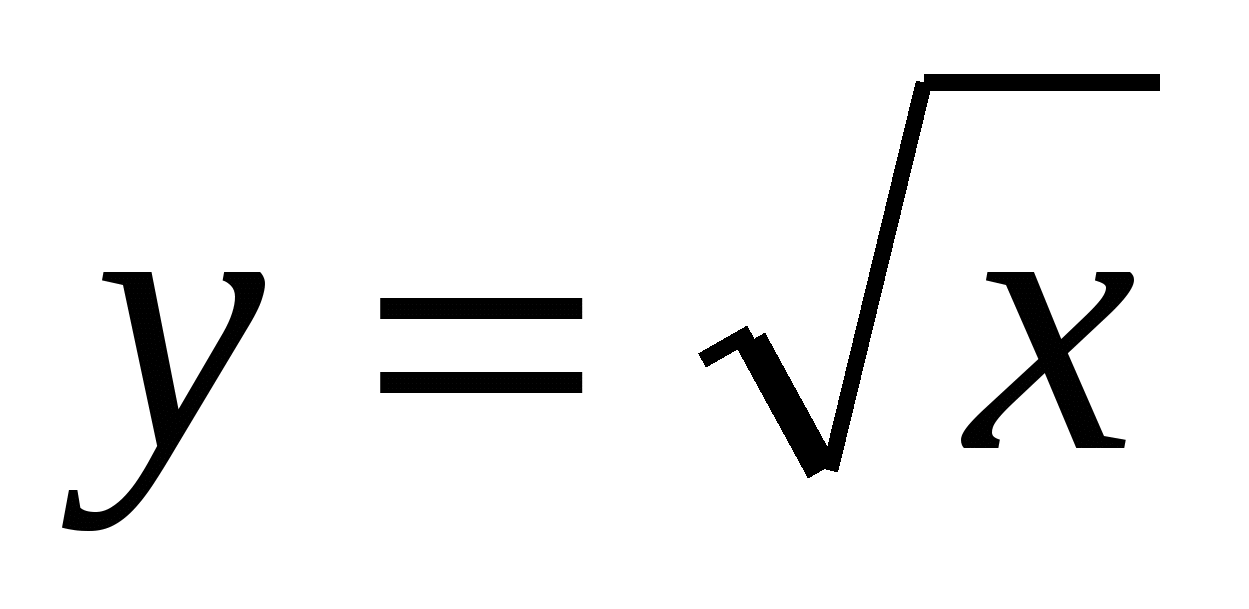 при решении различных задач при решении различных задач
|
Комбинированный урок
Практикум по решению задач
|
36
37
|
Ноябрь
|
Вычисление квадратного корень из произведения и дроби.
Квадратный корень из произведения и дроби при преобразовании выражений с корнем
|
Лекция
Практическая работа
|
|
Исследовать свойства квадратного корня.
Доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений.
|
|
|
38
39
40
|
Ноябрь
|
Квадратный корень из степени при вычислениях
Квадратный корень из степени в преобразовании выражений
Квадратный корень из степени в преобразовании выражений
|
Комбинированный урок
Практикум по решению задач
Консультация
|
41
|
Ноябрь
|
Контрольная работа №3 «Свойства арифметического квадратного корня».
|
Письменная контрольная работа
|
42
43
44
|
Ноябрь
|
Вынесение множителя из-под знака корня. Внесение множителя под знак корня.
Вынесение множителя из-под знака корня. Сокращение дробей, содержащих квадратные корни, освобождение от иррациональности в знаменателе дроби
|
Практические исследования
Комбинированный урок
Практическая работа
|
Доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений.
Вычислять значение выражений, содержащих квадратные корни; выражать переменные из геометрических и физических формул.
|
45
46
47
|
Ноябрь
|
Преобразование выражений, содержащих квадратные корни.
Решение различных задач с преобразованием выражений, содержащих квадратные корни.
Решение различных задач с преобразованием выражений, содержащих квадратные корни.
|
Практическая работа
Практикум
Консультация
|
48
|
Декабрь
|
Освобождение от иррациональности в знаменателе дроби.
|
Комбинированный урок
|
| | | |
|
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.