1 в направлении личностного развития
 Скачать 1.84 Mb. Скачать 1.84 Mb.
|
Контрольная работа №5Вариант 1 1. Вычислите: а)  ; б) 2 ; б) 2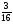 + 7 + 7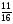 – 8 – 8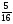 . .2. Выполните действия: а) 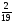 × 5; б) × 5; б) 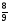 : 3. : 3.3О. Партия обуви, приобретенная предпринимателем, была продана за 3 дня. В первый день было продано  , а во второй , а во второй 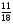 числа всех пар обуви. Какая часть обуви была продана в третий день? числа всех пар обуви. Какая часть обуви была продана в третий день?4О. За 3 ч из бассейна через одну трубу выливается 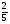 , а через другую – , а через другую – 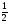 всей воды, находящейся в бассейне. Какая часть воды выльется из бассейна за 1 час, если открыть обе трубы одновременно? всей воды, находящейся в бассейне. Какая часть воды выльется из бассейна за 1 час, если открыть обе трубы одновременно?Вариант 21. Вычислите: а)  ; б) 3 ; б) 3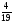 – 1 – 1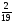 + 5 + 5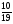 . .2. Выполните действия: а)  : 7; б) : 7; б) 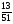 × 3. × 3.3О. За первую неделю бригада выполнила 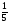 , а за вторую , а за вторую 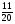 всей работы по строительству дома. Какую часть работы осталось выполнить бригаде? всей работы по строительству дома. Какую часть работы осталось выполнить бригаде?4О. Один экскаватор за день работы выкапывает 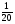 , а второй , а второй 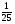 часть котлована. Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно? часть котлована. Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно? Вариант 3. 1. Вычислите: а) 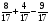 ; б) 4 ; б) 4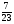 – 2 – 2 + 7 + 7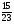 . .2. Выполните действия: а)  × 4; г) × 4; г) 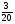 : 5. : 5.3О. На садовом участке были выращены огурцы, кабачки и тыквы. Масса огурцов составила 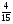 , а масса кабачков , а масса кабачков 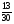 всей массы собранных овощей. Какую часть массы собранных овощей составили тыквы? всей массы собранных овощей. Какую часть массы собранных овощей составили тыквы?4О. Миша за 3 ч может вскопать 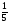 огорода, а его отец за это же время огорода, а его отец за это же время  огорода. Какую часть огорода могут вскопать Миша вместе с отцом за 1 час при одновременной работе? огорода. Какую часть огорода могут вскопать Миша вместе с отцом за 1 час при одновременной работе?Вариант 4 1. Вычислите: а)  ; б) 1 ; б) 1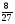 + 5 + 5 – 6 – 6  . .2. Выполните действия: а) 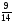 : 5; б) : 5; б) 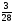 × 8. × 8.3О. За первую минуту спортсмен пробежал 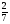 , а за вторую , а за вторую  дистанции. Какую часть дистанции ему осталось пробежать? дистанции. Какую часть дистанции ему осталось пробежать?4О. Для двух котельных был сделан запас угля. Одна котельная в течение месяца расходует  , а вторая , а вторая 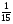 запаса угля. Какую часть угля израсходуют обе котельные за 4 месяца? запаса угля. Какую часть угля израсходуют обе котельные за 4 месяца?Контрольная работа №6Вариант 1 1. Начертите угол ABC, равный 160°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямую, перпендикулярную стороне BC. 2. В треугольнике ABC ÐА составляет 54°, а ÐC на 15° меньше. Найдите ÐB треугольника ABC. 3О. Вычислите: 201 × 15 – 7042 : 14. 4О. В двух мешках было 75 кг крупы. После того как из первого мешка продали 12 кг, а из второго 18 кг, в первом мешке крупы оказалось в 2 раза больше, чем во втором. Сколько килограммов крупы было в каждом мешке первоначально? Вариант 2 1. Начертите угол MNK, равный 150°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямую, перпендикулярную стороне NM. 2. В треугольнике ABC ÐА составляет 35°, а ÐB на 17° больше. Найдите ÐC треугольника ABC. 3О. Вычислите: 24 032 : 8 + 108 × 23. 4О. В двух цистернах было 30 т бензина. После того как из каждой цистерны продали по 6 т, в первой цистерне оказалось в два раза больше бензина, чем во второй. Сколько тонн бензина было в каждой цистерне первоначально? Вариант 3 1. Начертите угол MNK, равный 152°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямые, перпендикулярные сторонам угла MNK. 2. В треугольнике ABC ÐB составляет 14°, а ÐC в 3 раза больше. Найдите ÐA треугольника ABC. 3О. Вычислите: 637 637 : 91 – 207 × 12. 4О. В трех бидонах 80 л молока. После того, как из одного бидона отлили 8 л, а из другого 12 л, в каждом из них оказалось молока в 2 раза меньше, чем в третьем бидоне. Сколько литров молока было в каждом бидоне первоначально? Вариант 4 1. Начертите угол ABC, равный 146°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямые, перпендикулярные сторонам угла ABC. 2. В треугольнике ABC ÐА составляет 78°, а ÐB в 3 раза меньше. Найдите ÐC треугольника ABC. 3О. Вычислите: 145 261 : 29 – 103 × 47. 4О. В три овощных магазина завезли 1600 кг картофеля. После того, как в первом магазине продали 200 кг, а во втором и третьем по 100 кг картофеля, в третьем магазине его осталось в 2 раза больше, чем в каждом из первых двух. Сколько килограммов картофеля было в каждом магазине первоначально? Контрольная работа №7 Вариант 1 1. Вычислите: а) 5,7 + 2,34; б) 1,2 – 0,83. 2. а) Выразите в метрах: 15 дм; 3,4 см; 7 мм. б) Выразите в килограммах: 940 г; 7,2 т. 3. Длины сторон прямоугольника 1,2 дм и 25 см. Выразите их в метрах и найдите периметр прямоугольника. 4О. Мальчик поймал трех рыб. Масса первой рыбы 0,375 кг, масса второй на 20 г меньше, а масса третьей на 0,11 кг больше массы первой рыбы. Найдите массу трех рыб. 5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = a см, BC на 8,45 см меньше AB, а CD на 1,27 дм больше AB, и упростите его. Вариант 2 1. Вычислите: а) 6,83 + 15,3; б) 8,9 – 5,42. 2. а) Выразите в метрах: 3,2 дм; 543 см; 5 мм. б) Выразите в килограммах: 56 г; 2,7 т. 3. Длины сторон прямоугольника 3,8 дм и 54 см. Выразите их в метрах и найдите периметр прямоугольника. 4О. Яблоко, груша и апельсин вместе имеют массу 0,85 кг. Масса апельсина 360 г, а груша на 0,158 кг легче. Найдите массу яблока. 5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = х дм, BC на 12,71 см меньше AB, а CD на 2,85 дм больше AB, и упростите его. Вариант 3 1. Вычислите: а) 15,7 + 2,341; б) 17,3 – 8,562. 2. а) Выразите в метрах: 5 дм; 2,54 см; 0,57 мм. б) Выразите в килограммах: 0,32 г; 6,4 т. 3. Длины сторон треугольника 2,5 дм, 30 см, 120 мм. Выразите их в метрах и найдите периметр треугольника. 4О. Масса трех искусственных спутников 1,751 т. Масса первого спутника 6,6 ц, масса второго – на 73 кг больше. Найдите массу третьего спутника. 5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = у м, BC на 7,35 см меньше AB, а CD на 5,12 дм больше AB, и упростите его. Вариант 4 1. Вычислите: а) 1,683 + 12,9; б) 15,2 – 6,587. 2. а) Выразите в метрах: 3,2 дм; 36,8 см; 0,08 мм. б) Выразите в килограммах: 0,32 г; 6,4 т. 3. Длины сторон треугольника 5,1 дм, 29 см, 340 мм. Выразите их в метрах и найдите периметр треугольника. 4О. Слон, тигр и зубр вместе имеют массу 6,98 т. Масса слона 5,9 т, а тигр на 55,2 ц легче. Определите массу зубра (в килограммах). 5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = х м, BC на 2,93 см меньше AB, а CD на 4,31 дм больше AB, и упростите его. Контрольная работа №8Вариант 1 1. Вычислите: а) 8,3 ∙ 6; б) 2,06 ∙ 1,5; в) 9,76 : 3,2. 2. Найдите среднее арифметическое чисел 4,2; 4,1; 4,1; 4,3; 3,9. 3О. За 400 г сыра и 1,2 кг колбасы заплатили 126 р. 80 к. Какова цена1 кг колбасы, если 1 кг сыра стоит 95 р.? 4О. На двух складах было 210,2 т картофеля. После того как с первого склада было продано 24,5 т, а со второго 10,8 т, на первом складе картофеля оказалось в 2 раза больше, чем на втором. Сколько тонн картофеля было на каждом складе первоначально? Вариант 2 1. Вычислите: а) 3,4 ∙ 5; б) 3,08 ∙ 6,7; в) 7,8 : 1,2. 2. Найдите среднее арифметическое чисел 3,2; 4,5; 2,9; 3,1; 4,2. 3О. За 80 см шелка и 2,5 м шерсти заплатили 336 р. 40 к. Какова цена 1 м шерсти, если 1 м шелка стоит 58 р.? 4О. В двух бидонах было 51 л молока. После того как из первого бидона отлили 16,2 л, а из второго 7,2 л, во втором бидоне молока оказалось в 4 раза больше, чем в первом. Сколько литров молока было в каждом бидоне первоначально? Вариант 3 1. Вычислите: а) 78,56 ∙ 1,05; б) 46,508 : 1,51; в) 0,000135 : 2,7. 2. На соревнованиях по гимнастике двое судей оценили выступление спортсмена в 9,4 балла, трое в 9,5 балла и еще трое в 9,6 балла. Найдите средний балл спортсмена. 3О. За 600 г масла и 1,4 кг творога заплатили 103 р. 80 к. Какова цена1 кг творога, если 1 кг масла стоит 75 р.? 4О. В два магазина завезли 5,28 ц рисовой крупы. После того как в первом магазине продали 1,3 ц, а во втором 2,54 ц крупы, в первом магазине крупы осталось в 2 раза больше, чем во втором. Сколько центнеров крупы завезли в каждый магазин первоначально? Вариант 4 1. Вычислите: а) 2,06 ∙ 29,35; б) 51,456 : 1,28; в) 0,00245 : 3,5. 2. На соревнованиях по фигурному катанию трое судей выставили спортсмену оценку 5,4 балла, двое по 5,3 балла, еще двое по 5,5 балла и один – 5,6 балла. Найдите средний балл спортсмена. 3О. За 90 см ситца и 3,4 м полотна заплатили 148 р. 10 к. Какова цена 1 м полотна, если 1 м ситца стоит 21 р.? 4О. В двух коробках 1,77 кг конфет. После того как из первой коробки съели 0,56 кг, а из второй 0,91 кг конфет, во второй коробке конфет осталось в 3 раза меньше, чем в первой. Сколько килограммов конфет было в каждой коробке первоначально? Контрольная работа №9Вариант 1 1. Сметана содержит 20% жира. Сколько жира в 500 г сметаны? 2. В лесопарке посажено 15 кленов, что составляет 1% всех деревьев. Сколько деревьев в лесопарке? 3. Объем комнаты 45,36 м3, а площадь 16,8 м2. Найдите высоту потолка комнаты. 4О. С поля, засаженного капустой, в первый день было вывезено 58% урожая, а во второй – остальные 33,6 тонны. Сколько тонн капусты было вывезено с поля? 5О. Найдите массу 1 м3 сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 2,9 дм, 15 см и 0,8 м, имеет массу 281,88 кг. Вариант 2 1. Сыр содержит 35% жира. Сколько жира в 400 г сыра? 2. Петрушкой засеяно 3 м2, что составляет 1% площади огорода. Найдите площадь огорода. 3. Найдите высоту потолка спортивного зала, если его объем равен 5465,6 м3, а площадь пола – 854 м2. 4О. За первую неделю тротуарной плиткой было выложено 47% площади тротуара, а за вторую – остальные 561,8 м2. Какова площадь тротуара? 5О. Найдите массу 1 м3 кирпича, если один кирпич с измерениями 2 дм, 15 см и 0,1 м имеет массу 2,7 кг. Вариант 3 1. В состав нержавеющей стали входит 1,8% хрома. Найдите массу хрома в слитке стали массой 5 кг. 2. Сливки содержат 21,2% жира. Определите массу сливок, если в них содержится 74,2 кг жира. 3. До какого уровня залита вода в бассейн, имеющий форму прямоугольного параллелепипеда со сторонами 10,5 м и 30 м, если ее объем равен 787,5 м3? 4О. За первую неделю уборки урожая в саду было собрано 17% яблок, а затем остальные 20,418 т. Сколько тонн яблок было собрано в саду? 5О. Найдите массу 1 м3 сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 0,25 м, 8,5 см и 1,2 дм, имеет массу 20,655 кг. Вариант 4 1. Железная руда содержит 7,8% железа. Найдите массу железа в 3 т руды. 2. Сахарный тростник содержит 9% сахара. Сколько тростника потребуется, чтобы получить 144 кг сахара. 3. Найдите площадь поверхности воды в аквариуме, если 15 л воды заполняют его на 2,5 дм (1л = 1 дм3). 4О. За первую неделю было отремонтировано 54% площади дорожного покрытия, а за вторую – остальные 667 м2. Какова площадь отремонтированного дорожного покрытия? 5О. Найдите массу 1 м3 бетонного блока для фундамента, если один блок с измерениями 1,5 м, 4 дм и 60 см имеет массу 900 кг. Итоговая контрольная работа за курс 5 классаВариант 1 1. Вычислите: (8,3 + 4,72) ∙ (5,5 – 3,45). 2. Решите уравнение 3,5x = 7,21. 3. В первом овощехранилище на 5,6 т картофеля больше, чем во втором, а в двух овощехранилищах вместе 80 т картофеля. Сколько тонн картофеля во втором овощехранилище? 4. Постройте с помощью транспортира угол BAC, равный 35°, и отложите на луче AB отрезок AM длиной 6 см. Используя угольник, проведите через точку M прямую, перпендикулярную AC и пересекающую луч АВ. Найдите площадь образовавшегося треугольника (в м2). Ответ округлите до сотых. 5. После того как была продана четверть конфет, вес ящика с конфетами уменьшился на 24%. Определите массу пустого ящика, если ящик с конфетами имеет массу 60 кг. Вариант 2 1. Вычислите: (7,6 + 5,85) ∙ (10,9 – 4,86). 2. Решите уравнение 6,5x = 26,52. 3. На первом складе на 7,6 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на втором складе? 4. Постройте прямоугольник ABCD со сторонами AB = 5 см, AD = 8 см. Проведите луч AM, пересекающий BС в точке M так, чтобы угол BAM оказался равным 40°. Выполните необходимые измерения и найдите площадь образовавшегося треугольника BAM (в м2). Ответ округлите до сотых. 5. После того как была продана половина конфет, вес ящика с конфетами уменьшился на 45 %. Определите массу пустого ящика, если ящик с конфетами имеет массу 50 кг. Вариант 3 1. Вычислите: (6,4 + 7,72) ∙ (13,8 – 5,75). 2. Решите уравнение 2,5y = 12,65. 3. В первой канистре на 4,8 л бензина больше, чем во второй, а в двух канистрах вместе 60 л бензина. Сколько литров бензина в первой канистре? 4. Постройте с помощью транспортира угол BAC, равный 55°, и отложите на луче AС отрезок AM длиной 6 см. Используя угольник, проведите через точку M прямую, перпендикулярную AC и пересекающую луч АВ. Найдите площадь образовавшегося треугольника (в м2). Ответ округлите до сотых. 5. После того как была продана треть конфет, вес ящика с конфетами уменьшился на 32%. Зная, что полный ящик с конфетами весил 45 кг, определите, сколько весит пустой ящик. Вариант 4 1. Вычислите: (4,1 + 7,95) · (7,4 – 5,32). 2. Решите уравнение 5,5m = 38,72. 3. На первом складе на 9,8 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на первом складе? 4. Постройте прямоугольник ABCD со сторонами AB = 4 см, AD = 6 см. Проведите луч AM, пересекающий СD в точке M так, чтобы угол DAM оказался равным 25°. Выполните необходимые измерения и найдите площадь треугольника MAD (в м2). Ответ округлите до сотых. 5. После того как одна пятая часть конфет была съедена, вес коробки с конфетами уменьшился на 15%. Зная, что полная коробка весила 0,4 кг, определите, сколько весит пустая коробка. Тексты контрольных работ взяты из методического пособия: Зубарева И.И. Математика. 5-6 классы : методическое пособие для учителя / И.И.Зубарева, А.Г.Мордкович. – 3-е изд., испр. – М.: Мнемозина, 2008. |