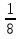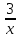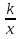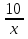Методическая разработка интегрированного урока по алгебре и информатике в 9 классе с использованием табличного процессора Ex с

Название	Методическая разработка интегрированного урока по алгебре и информатике в 9 классе с использованием табличного процессора Ex с
Дата	13.04.2016
Размер	178.05 Kb.
Тип	Методическая разработка

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Санкт-Петербургское училище олимпийского резерва №2 (техникум)»

Методическая разработка интегрированного урока по алгебре и информатике в 9 классе с использованием табличного процессора Exсel по теме: «Уравнения прямой, параболы, гиперболы»

Учебник: Ш.А.Алимова, Ю.М.Колягина, Ю.В.Сидорова Алгебра. 9 класс, М., Просвещение , 2010.

Составитель: Питленко Галина Георгиевна

учитель и преподаватель математики и информатики

ГБОУ СПО « Санкт-Петербургское училище олимпийского резерва №2 (техникум)»

Санкт-Петербург

2013

Введение

В настоящее время мировая тенденция образования предполагает переход процесса обучения на новый технологический уровень с обязательным использованием информационных технологий (ИТ). Использование ИТ позволяет решать следующие задачи:

повышает качество и эффективность обучения;
сокращает время изучения предмета;
укрепляет различные межпредметные связи, позволяя проводить интегрированные уроки;
значительно повышает интерес учащихся к изучаемой дисциплине.

Одной из конкретных форм применения ИТ является применение компьютера при изучении курса алгебры и подготовке учащихся 9-х классов к итоговой аттестации по теме «Уравнения прямой, параболы, гиперболы». Данный урок - интегрированный урок алгебры и информатики с использованием табличного процессора Excel 2007-2010

При рассмотрении тем, связанных с построением графиков и проверкой графических заданий, использование компьютера оправдано. При построении графиков на доске или в тетради основная часть времени и внимания учащихся тратится на формирование таблиц значений аргумента и функции. Использование технологии построения графиков в табличном процессоре Excel позволяет значительно сэкономить время на эту рутинную часть работы (которую учащиеся уже освоили ранее), увеличить объем материала, провести сравнении различных графиков, сделать работу над графиками интересной, яркой и зрелищной. Работа по исследованию свойств различных графиков при этом становится более доходчивой для учащихся.

Данный урок может быть адаптирован для изучения, обобщения и повторения материала по данной теме, а также для подготовки к итоговой аттестации учащихся по построению и исследованию графиков и решению уравнений графическим способом. Материалы урока можно использовать при внедрении в учебный процесс элементов дистанционного обучения

Цели урока:

Обучающая: закрепление навыков исследования функций и построения графиков прямой, параболы и гиперболы. Построение графиков функций в среде электронных таблиц; обобщение и систематизация знаний о свойствах функций.

Развивающая: развитие логического мышления, формирование поискового стиля мышления, умение сравнивать, анализировать, делать выводы.

Воспитательная: воспитание усидчивости, внимания; привитие учащимся навыков самостоятельной работы, бережного отношения к оборудованию.

Тип урока: обобщающий урок.

Вид урока: урок теоретических и практических работ исследовательского типа.

Форма работы: классно-урочная.

Технология: личностно-ориентированная; проблемно-исследовательская, информационно коммуникационная.

Время проведения: 2013 год.

Оборудование: компьютерный класс, интерактивная доска, мультимедийный проектор.

План урока:

1. Организационный момент.

2. Сообщение темы и постановка цели урока.

3. Фронтальный опрос для проверки уровня подготовки учащихся по свойствам графиков прямой, параболы и гиперболы.

4. Актуализация знаний по построению диаграмм и графиков с помощью табличного процессора Excel

5. Практическая самостоятельная работа на компьютере: построение графиков.

6. Обсуждение результатов.

7. Домашнее задание.

Ход урока:

1. Организационный момент. Приветствие.

2. Сообщение темы и постановка цели урока.

В первой части итоговой письменной работы чаще всего представлены задания, требующие установить соответствие между графиком и формулой, задающей функцию. Среди графиков функций встречаются прямые, параболы и гиперболы. Для выполнения заданий по этой теме из любой части работы полезно знать уравнения и свойства этих функций. Сегодня на уроке мы повторим и обобщим этот материал.

Мотивация.

Вы знаете, что для построения графиков вручную требуется много времени, приходится выполнять достаточно много вычислений, заполнять таблицу значений аргумента и функции. Поэтому сегодня мы будем строить графики с помощью табличного процессора MS Excel, который по нашей команде выполнит вычисления и построит графики. Нашей задачей будет повторение уравнений прямой, параболы и гиперболы, а также закрепление знаний по основным свойствам этих функций.

3. Фронтальный опрос для проверки уровня подготовки учащихся по свойствам графиков прямой, параболы, гиперболы.

Перечень вопросов и ответов для фронтального опроса и повторения.

№ п/п	Вопрос	Ответ
1	Что является графиком линейной функции?	Прямая
2	Как записывается уравнение прямой?	y = kx+b
3	В какой точке прямая y = kx+b пересекает ось Оу?	В точке с ординатой b
4	Как называется коэффициент k?	Угловой коэффициент
5	Когда две прямые y₁ = k₁x+b₁и y₂ = k₂x+b₂ параллельны?	Если k₁=k₂ и b₁= b₂
6	Когда две прямые y₁ = k₁x+b₁и y₂ = k₂x+b₂ пересекаются?	Если k₁= k₂
7	Чему равна ордината точки на оси абсцисс?	Ордината равна нулю
8	Чему равна абсцисса точки на оси ординат?	Абсцисса равна нулю
9	Что является графиком квадратичной функции?	Парабола
10	Как записывается уравнение параболы?	y=ax²+bx+c
11	Какой коэффициент называется старшим?	Коэффициент a
12	Как определить, куда направлены ветви параболы – вверх или вниз?	При а>0 – ветви вверх При а< 0 - вниз
13	Как найти координаты вершины параболы?	x_в= -b/2a y_в₌ ax²_в+ bx_в+ c
14	Как найти точки пересечения параболы: а) с осью Оу; б) с осью Ох?	Решив уравнения: а) y=a·0²+b·0+c; х=0, y=с; б) 0=ax²+bx+c; y=0

№ п/п	Вопрос	Ответ
15	Как определить количество точек пересечения параболы с осью Ох?	По дискриминанту D=b²- 4ac; D=0 одна точка пересечения, D>0 две точки пересечения, D<0 нет точек пересечения.
16.	Как называется график обратной пропорциональности у=k/x?	Гиперболой
17	Сколько ветвей имеет гипербола?	Две ветви
18	В каких частях координатной плоскости может располагаться гипербола?	В 1 и Ш, либо во П и 1V
19	От чего зависит расположение гиперболы?	При k>0 ветви гиперб. в 1 и Ш четв. При k<0 во П и 1V

Повторение общей схемы исследования функции и построения ее графика.

№ п/п	Вопрос	Ответ
1	Что такое область определения функции D(f)?	Множество всех значений, которые может принимать ее аргумент.
2	Что такое область значений функции E(f)?	Все значения, которые принимает функция при х, принадлежащем D(f)
3	Что такое четная функция?	Функция четная, если для любого х из D (f) выполняется равенство у(-х)=у(х)
4	Что такое нечетная функция?	Функция нечетная, если для любого х из D (f) выполняется равенство у(-х)=-у(х)
5	Какая функция называется возрастающей?	Если у(х₂)>у(х₁) при х₂>х₁, то функция возрастающая на этом промежутке.
6	Какая функция называется убывающей?	Если у(х₂)<у(х₁) при х₂>х₁, то функция убывающая на этом промежутке.

4. Актуализация знаний по построению диаграмм и графиков с помощью табличного процессора Excel

Метод повторения – словесно-иллюстративный в форме практического занятия с использованием интерактивной доски.

Ввод формулы начинается со знака «=». Формулы содержат числа, имена ячеек, знаки операций, круглые скобки, имена функций. Формула пишется в одну строку, символы выстраиваются последовательно друг за другом, проставляются все знаки операций. Повторим знаки операций:

+ сложение, - вычитание; * умножение; / деление; ^ возведение в степень.

Для распространения данных и формул используется маркер заполнения, для этого:

1. Выделите ячейку (или две соседние ячейки для распространения значений с заданным интервалом)

2. Установите указатель в правый нижний угол и, когда он примет вид тонкого черного креста, удерживая нажатой левую клавишу мыши, перетащите его в нужном направлении.

Алгоритм построения графиков функций в табличном процессоре Excel:

1 . Ввести значение аргумента с заданным промежутком.

2. Ввести формулу (уравнение функции)

3. Распространить данные и формулу с помощью маркера заполнения.

4. Построить график функции (вставка – диаграмма – точечная), выделив диапазон значений.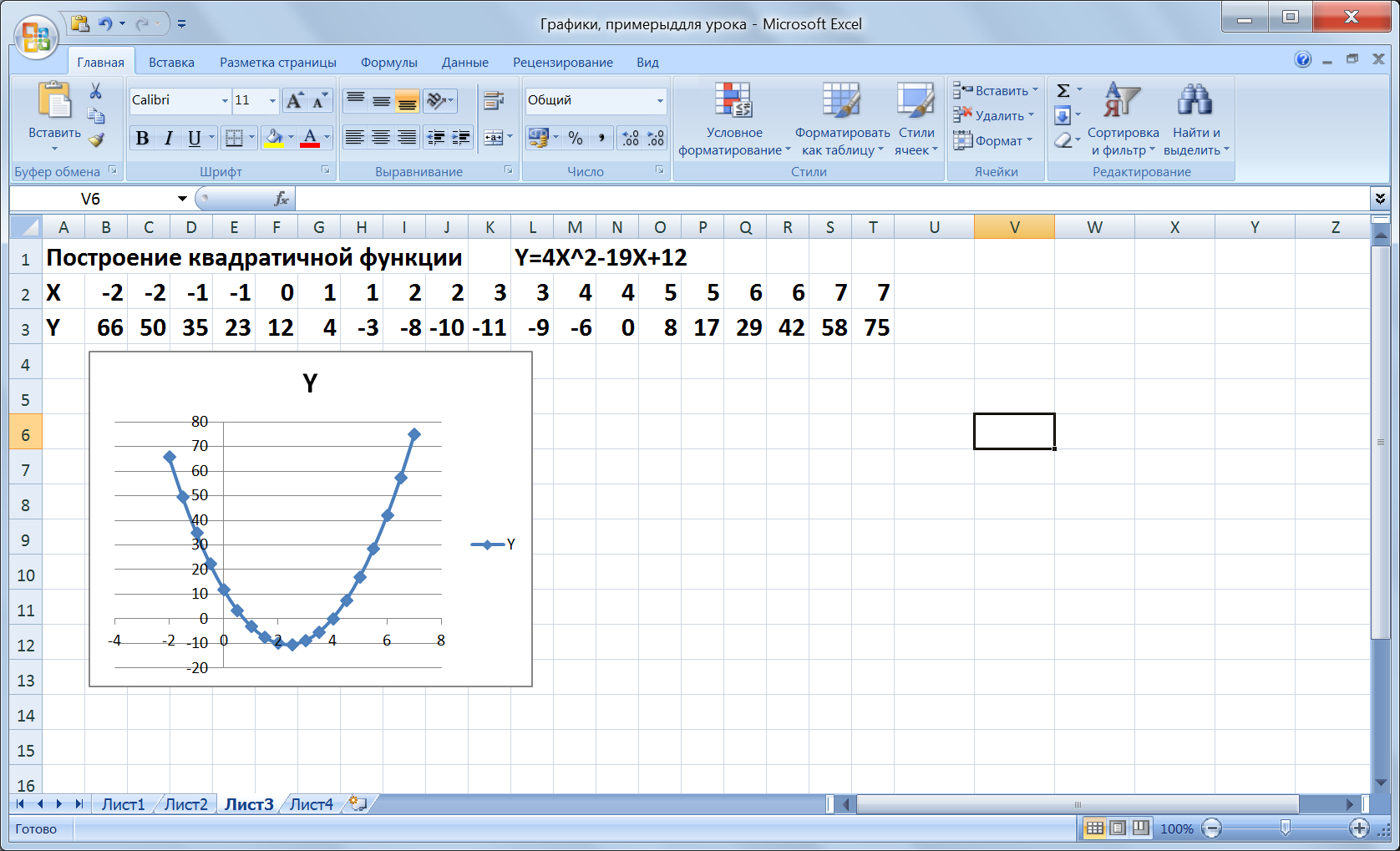

5. Практическая самостоятельная работа на компьютере: построение графиков прямой, параболы и гиперболы.

Задания для работы и результаты работы учащихся передаются по локальной сети на сервер преподавателя. Задания дифференцированы по сложности. Учащиеся работают в индивидуальном режиме. Используя сетевые ресурсы, преподаватель контролирует работу учащихся на всех этапах.

Примеры заданий.

№ п/п	Задание	Ответ
1	Даны уравнения прямых: а) y=-x+2; б) y = 5x-2; в) y = 3x-2; г) y = 5x-3; д) y = 4x-3; е) y = 2x-4. Найти и построить: параллельные прямые; пересекающиеся прямые.	Параллельные б), г) Пересекающиеся – все остальные.
2*	Построить график прямой, проходящей через точки с координатами (2;0) и (0;2)	y=-x+2
3*	Прямая y = kx+b пересекает ось Ох в точке (-2;0) и ось Оу в точке (0;6). Построить график этой прямой. Проходит ли эта прямая через точку (1;9)?	y = 3x+6; Да, проходит.
4	Даны уравнения парабол: а) y=-x²+2x+5; б) y=1,5x²+3x+3,5; в) y=4x²+12x+9; г) y=x²-3x-4; д) y=2x²-4x+1; Построить параболу: с ветвями вниз. С одной точкой пересечения с осью Х С двумя точками пересечения с осью Х Без точек пересечения с осью Х.	а) y=-x²+2x+5; в) y=4x²+12x+9; г) y=x²-3x-4; б) y=1,5x²+3x+3,5;
5*	При каком значении k парабола касается оси абсцисс? а) y=2x²-4x+ k; б) y=2x²+3x+ k; Построить эти параболы	а) y=2x²-4x+2; б) y=2x²+3x+1;

№ п/п	Задание	Ответ
6	Даны уравнения: а) y=; б) y=; в) y=; Построить график в 1 и Ш четверти; Построить график во П и 1V четверти.	а) y=; в) y=; б) y=;
7*	Графику y= принадлежит точка (-2;-5) В каких четвертях он расположен?	y=; в 1 и Ш четверти
8*	Графику функции y= принадлежит точка (-10;-0,3)? Построить этот график	Да, принадлежит.

Задания со * - из второй части письменной работы.

6. Обсуждение результатов. Сравнить результаты построения графиков на компьютере и вручную. Оправдано ли при построении данных графиков и применение компьютера? Сделать выводы.

Анализ полученных результатов. Выставление комплексных оценок: за фронтальный опрос и практическую работу.

7. Домашняя работа. Повторение общей схемы исследования функции и построения ее графика. Результаты занести в таблицу.

Название	Формула	Основные свойства	График
Прямая
Парабола
Гипербола

Список литературы и Интернет-ресурсов:

Кочагин В.В. ГИА 2013 Математика: сборник заданий: 9 класс – М; Эксмо,2012
https://do.gendocs.ru/docs/index-144410.html
https://uchmet.ru/library/material/144058/
https://metod-kopilka.ru/page-2-2.html
geometry2006.narod.ru