«Применение коррекционно-развивающих упражнений на уроках и во внеклассной работе по математике»
 Скачать 203 Kb.
|
| МС(К)ОУ «Специальная (коррекционная) общеобразовательная школа VIII вида» Обобщение опыта по теме: «Применение коррекционно-развивающих упражнений на уроках и во внеклассной работе по математике» Учитель математики Трухина Татьяна Борисовна г. Мичуринск, 2010 Задача специальной (коррекционной) школы состоит в том, чтобы создать такую модель обучения детей с ОВЗ, в процессе которой у каждого обучающегося появится механизм компенсации имеющегося дефекта, на основе чего станет возможной его интеграция в современное общество. Система коррекционно-развивающего обучения направлена на разностороннее развитие личности учащихся, способствует их умственному развитию. На сегодняшний день в области специального образования одной из основных проблем является проблема поиска наиболее эффективных условий организации обучения детей с ОВЗ. Своеобразие познавательной деятельности учащихся специальных (коррекционных) общеобразовательных школ VIII вида, по мнению многих педагогов (В.В.Эк, М.Н.Перова, Е.Д.Худенко и др.) определило коррекционную направленность их обучения математике. Практика школьного обучения и наблюдения за математическими навыками учащихся с ОВЗ свидетельствуют о недостаточном уровне сформированности математических знаний, что выражается в типовых ошибках, бедном и зачастую, недифференцированном словаре, слабых вычислительных навыках и т.д. Для эффективного усвоения учебной программы необходимы специальные упражнения, предполагающие комплексную работу сразу нескольких анализаторов. Проблема заключается в том, что в коррекционной подготовке не существует готовых коррекционно-развивающих упражнений, направленных на развитие ВПФ у детей с ОВЗ, либо выполняющих компенсаторную функцию, а использование просто дидактических приемов и методов передачи учебной информации не всегда позволяет справиться с поставленной задачей. Рассмотрим коррекционно-развивающие упражнения, которые можно использовать на уроках и во внеклассной работе по математике. Задания на развитие познавательной активности. В своей работе я широко использую задачи практического характера и задачи, интересные в познавательном отношении. Их я составляю на основе цифровых данных материалов газет, журналов, статистических справочников и энциклопедий. Простые задачи чаще всего для устного счета. Задачи более сложные использую для индивидуальной работы с сильными учениками.
Задания на развитие внимания. Внимание – это самый первичный познавательный процесс, с которым рождается ребенок, благодаря которому он удивляется новизне окружающего мира и творчески исследует его. Для развития этого вида творческой деятельности можно использовать всевозможные лабиринтные задания, задания-путаницы, разнообразные игры, требующие от ученика для их правильного выполнения сосредоточенности, наблюдательности, усидчивости.
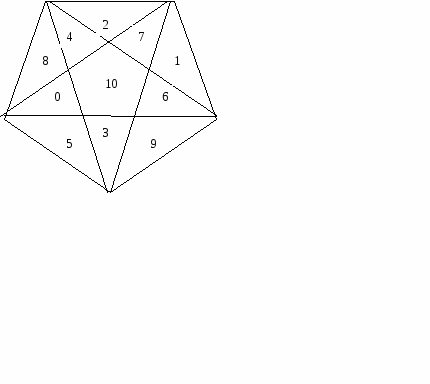 Назовите и покажите все числа от 1 до 10 по порядку. Назовите все однозначные (двузначные) числа, которые здесь встречаются. Чем двузначные числа отличаются от однозначных?
В одном городе жили-были неразлучные друзья: Коля, Толя, Миша, Сережа. Коля – самый высокий, Толя – самый толстый, Миша – самый тонкий, Сережа – самый низкий. Теперь скажите, кто самый толстый? Самый низкий? Самый высокий? Самый тонкий?
В одном городе на одной площадке стояли два больших дома. В одном доме жили лиса, волк, коза. В другом доме жили белка, баран, лошадь. Однажды вечером лиса, волк и коза решили позвонить своим соседям. Узнайте кто кому звонил. 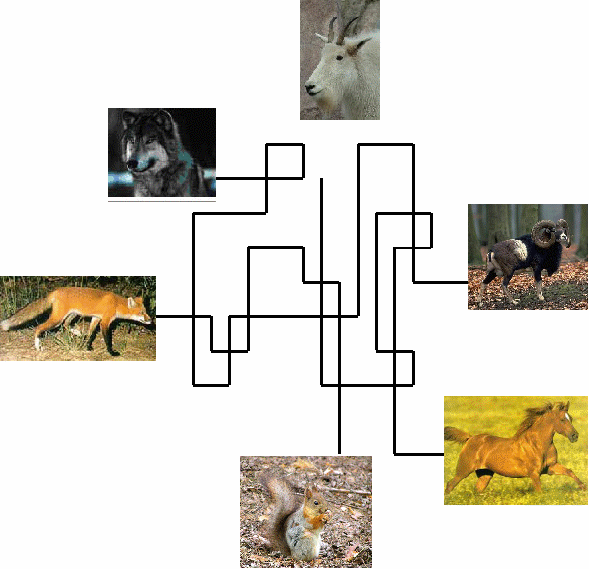  Задачи на развитие памяти. Развитие произвольной памяти – одна из главных задач современной школы. Для формирования произвольного запоминания можно использовать задания на основе геометрического и счетного материала. Детям предлагается зрительно или на слух запомнить как можно больше фигур и чисел или порядок их расположения и нумерацию. Задания можно усложнить путем введения большого числа предметов, которые надо запомнить.
В жизни на приходится часто запоминать адрес, номер телефона, посчитать деньги при покупке. И всегда в этих случаях нам надо запомнить числа. Вот и сейчас мы будем запоминать числа на слух. Я вам их медленно прочитаю, а вы должны их затем назвать, не нарушая порядка следования: 1, 7, 9, 2, 3, 5.
Учитель показывает треугольники и круги, не придерживаясь ни какого порядка, учащиеся должны запомнить, сколько увидели треугольников и сколько кругов. Те, кто правильно запомнил, считаются победителями. Теперь учитель вводит в игру квадраты (далее аналогично). Затем и прямоугольники (далее аналогично).
З  апомните как можно больше фигур и зарисуйте их.
Давайте поиграем. Я буду ставить точки в фигуры, а вы должны запомнить, как я это делаю, и повторить за мной.  Задания на развитие мышления. Для развития творческого мышления большое значение имеют задания, ориентирующие школьников на получение нового продукта. Задания подобного вида наиболее ярко показывают уровень развития творчества каждого ребенка, так как учащиеся пробуют создать что-то новое, свое, неповторимое, используя для этого усвоенные ранее знания и умения. К упражнениям такого вида можно отнести такие задания: составление задач и выражений, нахождение своего способа действия, постановка дополнительных вопросов к заданию учебника, придумывание предметов на основе заданных геометрических фигур.
С числами 15 и 4 составьте два задании так, чтобы одно из них было задачей, а другое – нет.
Нужно из всех кружков убрать белые. Как это можно изобразить на рисунке? Я это сделала так:  Нарисуй свой способ.
Составь задачу по её решению: 32 – 20. Если можете, то запишите все возможные вопросы к условию задачи так, чтобы решение не изменялось.
Помогите художнику дорисовать картинки. Например, был овал – стал зайчик, был овал – стала ложка и т.д. Задания на развитие воображения. Здесь необходимо фантазировать, мысленно представлять итоги того или иного преобразования, например, вообразить целое из предложенных его частей, соотнести размеры на глаз, придумать человечка или зверька из предложенных геометрических фигур и т.д. 1. «Кто лучше?» 3  -4 ученика, зажмурившись, чертят одновременно на доске одну и ту же геометрическую фигуру: Выбывает из игры то, кто начертил хуже других. (аналогично с усложняющимися фигурами).
Нарисуйте веселого человечка, используя фигуры:  
Из одних кругов разного размера нарисуйте петушка.
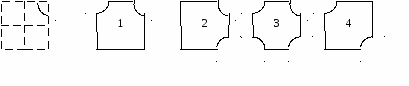 В начале ряда нарисована бумажная салфетка, свернутая вчетверо. После того, как салфетку свернули, в ней сделали фигурный вырез. Необходимо определить, как будет выглядеть салфетка, если её развернуть. Из четырех готовых ответов выберете правильное решение и запишите номер решения. 5. «Угадай». 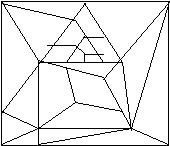 Как вы думаете, что получится на Машином рисунке, если все треугольники раскрасить, а оставшиеся четырехугольники – зеленым? Проверь свою догадку. Задания на смекалку. Для подбора заданий на смекалку имеется самая большая литература. Сюда относятся задачи-шутки, головоломки, ребусы, занимательные вопросы и т.д. Подобные задания способствуют разностороннему развитию умственной деятельности детей, так как учащиеся пробуют сопоставлять, менять местами, находить подходящие варианты.
Летели гуси: один гусь впереди, а два – позади; один – позади, два – впереди; один между двумя. Сколько всего летело гусей? Как они летели? Сделайте рисунок.
Учитель расставляет на листе бумаги несколько предметов разной величины и формы и обводит их цветным карандашом. Затем все эти предметы кладет на те места, где они обычно находятся. После этого вызывает детей, которые должны по получившимся контурам догадаться, какие здесь обведены предметы, отыскать их и поставить на контуры. Те из играющих, кто правильно закроет большее число контуров, считается победителем.
Пятью прямыми линиями разделите циферблат так, чтобы в каждой части числа давали бы равную сумму. 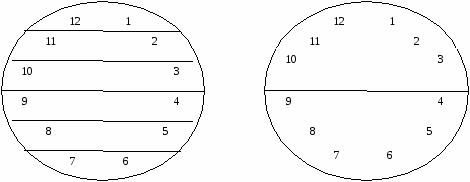 Задачи на сообразительность.
Задания на нахождение альтернативных вариантов. В жизни человеку часто приходится искать несколько путей решения одной проблемы. Но он не задумывается о том, что тем самым участвует в творческом процессе. Учащимся нужно овладевать приемами альтернативы, чтобы суметь увидеть различные подходы к решению математических задач и выражений. Здесь же можно предлагать ребятам выбрать один или несколько правильных вариантов из множества предложенных или способы их решения. 1. Расположите цифры 1, 2, 3 в разном порядке. Найдите все 6 способов. 2. «Смекай». М 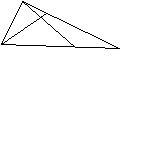 иша получил в школе задание: провести в треугольнике две линии. Он выполнил задание.А теперь задание для вас. Как по-другому можно провести две линии внутри треугольника? 3. «Шесть стульев». Миша готовил класс к утреннику. А Маша решила, пользуясь случаем, дать ему выполнить задание. Она попросила его расставить шесть стульев у четырех стен комнаты по-разному. Как Миша мог бы выполнить задание Маши? 4 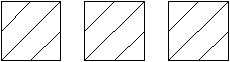 . «Раскрась».Раскрась квадраты так, чтобы два из них были одинаковыми, а два – разными. 5. «Разноцветные шарики». В коробке было 3 желтых и 3 красных шарика. Миша взял 4 шарика. Сколько шариков каждого цвета могло быть у Мальчика? Найди три ответа. Сколько шариков осталось в коробке? 6. «Найди все дороги». Представьте, что это кружок – ваш велосипед и вам надо проехать из левого нижнего угла в правый верхний. Но одно условие – каждый раз вы должны ехать по разным дорожкам.  Задания на использование анализа. Умение анализировать – одна из главных особенностей творческой деятельности. Анализ – это метод научного исследования путем рассмотрения отдельных сторон, свойств, составных частей чего-либо. Он может быть мыслительным, мысленно-зрительным. Ребятам можно предлагать задания на нахождение недостающей фигуры, определение последовательности, на зрительное восприятие точечного рисунка, на нахождение закономерности между рисунком и записью и др. 1. «Логическая задача». У девочки было три мяча – красный, синий и зеленый. Красный был больше, чем синий, а синий больше, чем зеленый. Какой мяч самый большой? Какой самый маленький? Нарисуй мячи в порядке увеличения их размеров и закрась нужным цветом. 2. «Раскрась кубики». 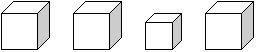 Надо раскрасить большие кубики так, чтобы маленький кубик был между желтым и зеленым, а черный был рядом с желтым. 3. «Недостающая фигура». Н 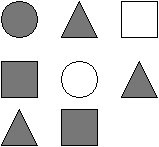 арисуй недостающую фигуру и закрась её нужным цветом.4. «Точечный рисунок». 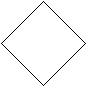 . . . . . . Нарисуй по точкам такую же фигуру.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Задания на нахождение или выбор удобного способа действия. Суть упражнений на выбор удобного способа действия заключается в том, что учащиеся ставятся в трудное положение: им нужно из нескольких верных ответов выбрать наиболее удобный. В рамках этого вида творческого задания дети пытались находить удобное направление движения, удобное решение, самый легкий и удобный путь до поставленной цели. 1. «Раздели яблоко поровну». Раздели яблоко 6 ребятам, чтобы никого не обидеть. 2. «Удобный способ вычисления». Найдите значения выражений удобным способом: 30 + 2 + 40 + 5 = 9 + 7 + 1 = (98 + 98) – 98 = 10 + 7 + 2 = 8 + 2 + 5 = (26 + 76) – 26 = 6 + 30 + 20 = 2 + 7 + 8 = (37 + 43) – 43 = 70 + 9 + 10 = 3. «Поднимись по лестнице». Мише надо подняться по лестнице, которая состоит из 9 ступенек. Когда быстрее Миша доберется до площадки, если не будет пропускать ступенек? Будет прыгать через одну, через две ступеньки? Почему? 4 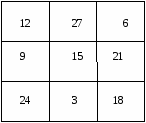 . «Как удобнее?»Как удобнее сложить тройки чисел, чтобы проверить, что квадрат – магический? 5. Вы находитесь в зрительном зале. Вам нужно место № 4. В ряду 9 мест:  С какой стороны (слева или справа) вы найдете быстрее свое место? Задания на умение классифицировать. Классифицировать – это значит суметь распределить по группам, разрядам или классам. Основой этого типа задания является умение выделять признаки предметов и устанавливать между ними сходства и различия. Можно предлагать детям разные варианты формулировки подобных упражнений. В одних на основание классификации указывает учитель, в других – дети сами выделяют эти основания. Детьми классифицируются предметы по признакам: размер, форма, цвет; числа: двузначные и однозначные, четные и нечетные; геометрические фигуры: треугольники, квадраты, круги, прямоугольники; линии: кривые, ломаные, отрезки. В более трудных случаях основание на классификацию содержит в себе 2 и более признака. 1. «Числа и фигуры». От однозначных чисел проведите стрелки в овал, от чисел, оканчивающихся нулем – в круг, от двузначных чисел – в полукруг. 7 4 16 18 10 6 3 14 2 11 19    8 0 12 5 9 17 13 1 20 15 2. «Игра в выражения». 37 + 0 = 72 + 2 = 10 + 40 = 15 + 0 = 20 + 30 = 26 + 1 = 50 + 20 = 6 + 3 = 99 + 0 = Распределите выражения на три группы. Найдите значения выражений. 3. «Игра в числа». Разбейте числа на две группы так, чтобы в каждой группе были числа, похожие между собой: 63, 8, 1, 30, 45, 6, 7, 10, 9, 99, 2, 74 4. «Фигуры». По какому признаку все фигуры можно разбить на 2 группы, 3 группы, 5 групп? 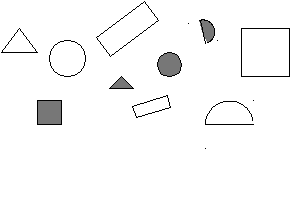 Задания на умение сравнивать. На первый взгляд простая операция сравнения включает в себя несколько ступеней:
Задания на умение сравнивать, это такие, где надо дорисовать недостающие части предмета, сравнить записанные выражения, не вычисляя их значения, найти схожее и отличительное в записи того или иного упражнения, сравнить выполненные на доске рисунки. 1. «Хватит ли?» 3 девочки и 4 стула. Хватит ли стульев? 7 учеников и 6 ручек. Хватит ли ручек? 5 малышей и 7 пар варежек… 8 петель и 9 пуговиц… 2. «Сравни». С 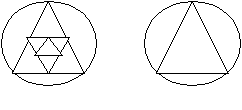 равните два рисунка, дорисуйте второй рисунок так, чтобы он стал одинаковым.3. Сравните выражения в каждой строке. Поставьте между ними знаки сравнения, не находя значений выражений. 9 + (1 + 7) 9 + (7 + 1) 8 + (6 + 2) (8 + 6) + 2 7 + (3 + 8) (7 + 3) + 8 4. «Сравни выражения». Выполните действия и скажите, чем все выражения слева отличаются от всех выражений справа? 5 + 2 + 1 = 5 + 2 + 2 = 4 + 1 + 2 = 4 + 1 + 3 = 1 + 2 + 1 = 1 + 3 + 1 = 2 + 2 + 1 = 2 + 2 + 2 = Задания на умение обобщать. Задания на обобщение включают в себя умение из множества чисел, слов, выражений, предметов и др. выделить «лишнее». Для устного выполнения творческих заданий этого типа детям приходится и сравнивать, и анализировать, и использовать элементы классификации, и только затем на основе всего этого дела выводы. От них требуется не только назвать или указать «лишний» предмет, «лишнее» число и др., но и обосновать свой выбор. 1. «Назовите одним словом». четыре квадрат двадцать треугольник один круг пятьдесят прямоугольник 2. «Лишнее слово». Выпишите лишнее слово: десять, два, пятнадцать, семьдесят, декабрь, восемь. 3. «Смекай-ка». 37, 7, 25, 15, 3, 11, 65, 45, 55, 10, 75, 85, 95 Выпишите все числа, которые схожи между собой по одному признаку, исключая «лишние» числа.
п  рямая______дм__ см_____минус замкнутая_____равнолиния длина длина знак линия знак 5. «Какая фигура лишняя». 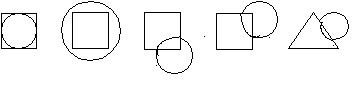 Среди изображенных пяти фигур четыре имеют в чем-то сходство, а одна от них отличается. Найдите эту «лишнюю» фигуру. Чем она отличается от остальных? Задания на установление взаимосвязей и соответствий. Этот тип заданий – один из наиболее сложных для детей с нарушением интеллекта. Найти соотношение, выражающее согласованность, равенство в каком-либо отношении довольно трудная задача порой даже для взрослых. Учащиеся предлагается в рамках этого вида заданий найти соответствие между парами выражений, частями предмета, найти недостающую часть изображения, раскрасить по аналогии предметы и т.д. 1. «Соответствия». Найдите соответствия между двумя числами и одной фигурой.
2. «Загадки веселого карандаша». Прочитайте слоги по порядку и отгадайте загадку.  2 1 4 3 6 5 8 7 9маль пять ков чи чу пять чи лан ков 3. «Составь домик». Н  айдите к каждому домику его крышу. При каким признакам вы ориентировались?Задания на установление последовательности и использование зачатков планирования. Творческие задания на установление последовательности очень редко встречаются в методической литературе. Чтобы научить детей находить логически обоснованные, закономерно вытекающие пути решения данных упражнений, учителю надо потрудиться самому, составляя и находя эти задания, посильные для детей. Это задания, где учащимся надо расставить картинки в определенном порядке, заполнить «шведскую стенку», постепенно выполняя действия, подняться по математической лесенке с «секретом», определить порядок действий, найти последовательность перехода по лабиринту. 1. «Расположи шарики в последовательности увеличения размера» (в последовательности изменения цвета: красный, коричневый, синий, оранжевый). Сколько шариков всего? Менялось ли количество шариков от того, что мы по-разному их размещали? 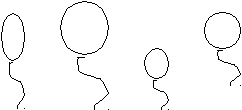 2. «Интересное задание». Используя данную закономерность, продолжи ряд чисел: 1, 3, 5, 7…. 3. «Ромашки». Расположи ромашки по порядку. 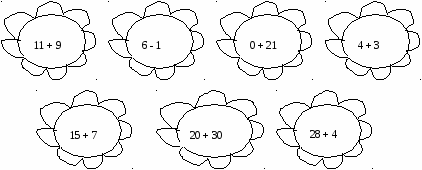 Использование коррекционно - развивающих упражнений в практике решает задачи обучения детей с особыми образовательными потребностями, а также является средством самообразования и саморазвития учителя. В заключении хочется отметить, что изучение математики должно обогащать ум и душу ребенка, помогать нашим маленьким гражданам жить полноценной, богатой духовно и успешной жизнью сейчас и быть способным в будущем найти свое достойное место в этом сложном, меняющемся мире. Информационные источники
|
, 3
, 6