|
201_ год
Рабочая программа учебного курса по предмету___МАТЕМАТИКА_______________________________
КЛАССЫ
|
11
|
|
|
ПЕДАГОГ
|
Ратникова Ольга Валентиновна
|
КОЛИЧЕСТВО ЧАСОВ
|
По программе в год:_________________ В неделю:________________________ ______________________
|
ПЛАНОВЫХ КОНТРОЛЬНЫХ УРОКОВ
|
|
|
|
ЗАЧЕТОВ
|
|
|
|
ТЕСТОВ
|
|
|
|
ЭКСКУРСИЙ
|
|
|
|
АДМИНИСТРАТИВНЫХ КОНТРОЛЬНЫХ УРОКОВ
|
|
|
|
УЧЕБНАЯ ПРОГРАММА СОСТАВЛЕНА НА ОСНОВЕ
|
Нормативных документов Министерства образования РФ «Примерные программы по математике», Москва, Дрофа, 2009 г
|
УЧЕБНИК
|
|
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ СОСТАВИЛ(А)
|
|
Пояснительная записка
Рабочая программа (полного) общего образования по курсу математики 11 класса составлена в соответствии с Федеральным компонентом государственного стандарта основного общего образования по математике, на основе примерной программы по предмету «Математика», утвержденной Министерством образования РФ, с учетом рекомендаций авторских программ А.Г.Модковича по алгебре и началам анализа и Л.С.Атанасяна по геометрии и рассчитана на 175 часов (5 часов в неделю).
Программа курса способствует логическому развитию и формирует умения пользоваться определенными алгоритмами.
Отличительной особенностью программы является изложение в ней учебного материала с учетом его усвоения. В рабочей программе определены цели в целом и по каждой теме, прогнозируются результаты их достижения в соответствии с уровнем содержания учебного материала. Закладываются основы для изучения курсов стереометрии в геометрии старших классов, физики, химии и других смежных предметов.
Цели программы:
формирование представлений о математике как универсальном языке;
развитие логического мышления, пространственного воображения, алгоритмической культуры;
понимание значимости математики для научно-технического прогресса;
систематическое изучение свойств геометрических тел в пространстве;
освоение способов вычисления практически важных геометрических величин;
научить владеть новыми понятиями, переводить аналитическую зависимость в наглядную форму и обратно.
дальнейшее развитие логического мышления учащихся.
Основные задачи:
В результате изучения курса математики учащиеся должны:
научить работать с книгой;
базировать изучение курса стереометрии в сочетании наглядности и логической строгости;
осуществлять индивидуальный подход к учащимся;
сформировать устойчивый интерес к предмету;
обеспечить прочное и сознательное овладение системой знаний и умений.
Формы организации образовательного процесса:
индивидуальные,
групповые,
индивидуально-групповые,
фронтальные,
классные и внеклассные.
Виды и формы контроля:
промежуточный,
текущий и итоговый,
индивидуальный,
фронтальный: тесты, математические диктанты, самостоятельные и контрольные работы, творческие задания, исследовательские задания.
Требования к уровню подготовки учащихся
В результате изучения курса математики 11 класса учащиеся должны:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем.
распознавать на чертежах и моделях пространственные формы; соотносить трёхмерные объекты с их описанием, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач.
Основное содержание программы
АЛГЕБРА
Первообразная и интеграл - 9 ч
Определение первообразной. Правила отыскания первообразных. Неопределенный интеграл. Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона – Лейбница. Площадь криволинейной трапеции.
Контрольная работа №1 по теме «Первообразная и интеграл»
Знать:
- определение первообразной;
- правила отыскания первообразных;
- формулы первообразных элементарных функций;
- определение криволинейной трапеции.
Уметь:
- вычислять первообразные элементарных функций, применяя правила вычисления первообразных;
- вычислять площадь криволинейной трапеции.
Степени и корни. Степенные функции – 20 ч
Определение корня n-ой степени четной и нечетной степени.
Решение иррациональных уравнений. Определение степени с рациональным показателем. Преобразование выражений, содержащих степени с рациональным показателем.
Применение свойств корня n-ой степени при преобразовании иррациональных выражений. Свойства функции 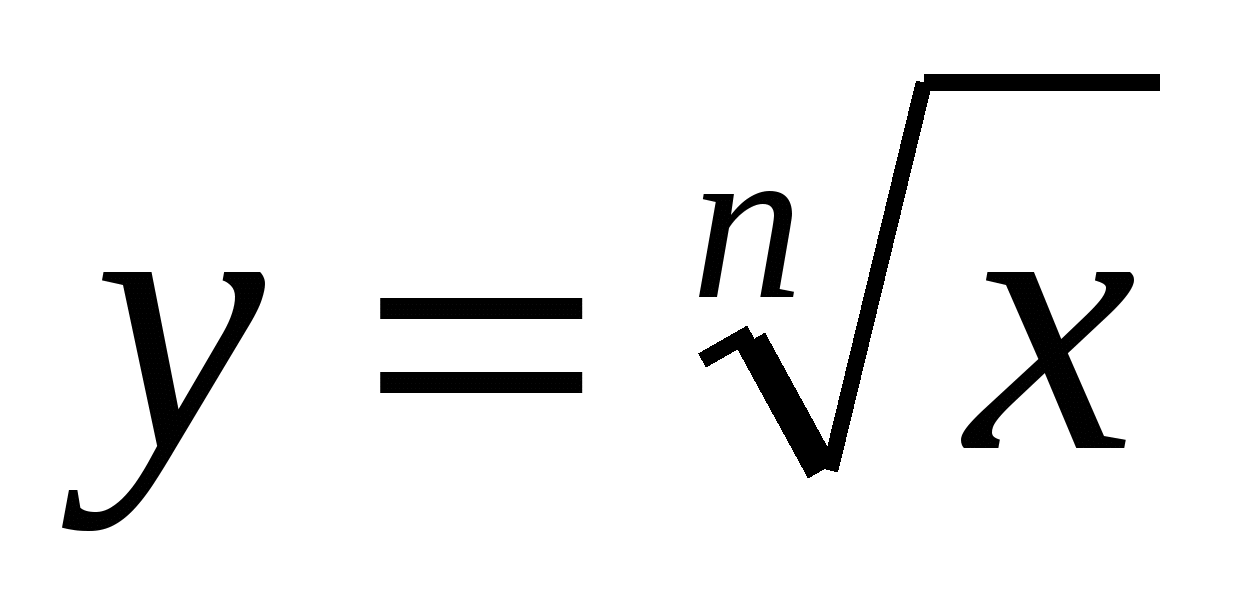 при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени. Свойства степенных функций в зависимости от показателя. при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени. Свойства степенных функций в зависимости от показателя.
Контрольная работа №4 по теме «Корень n-ой степени»
Контрольная работа №5 по теме «Степенные функции»
Знать:
- свойства корня n-ой степени; свойства функции 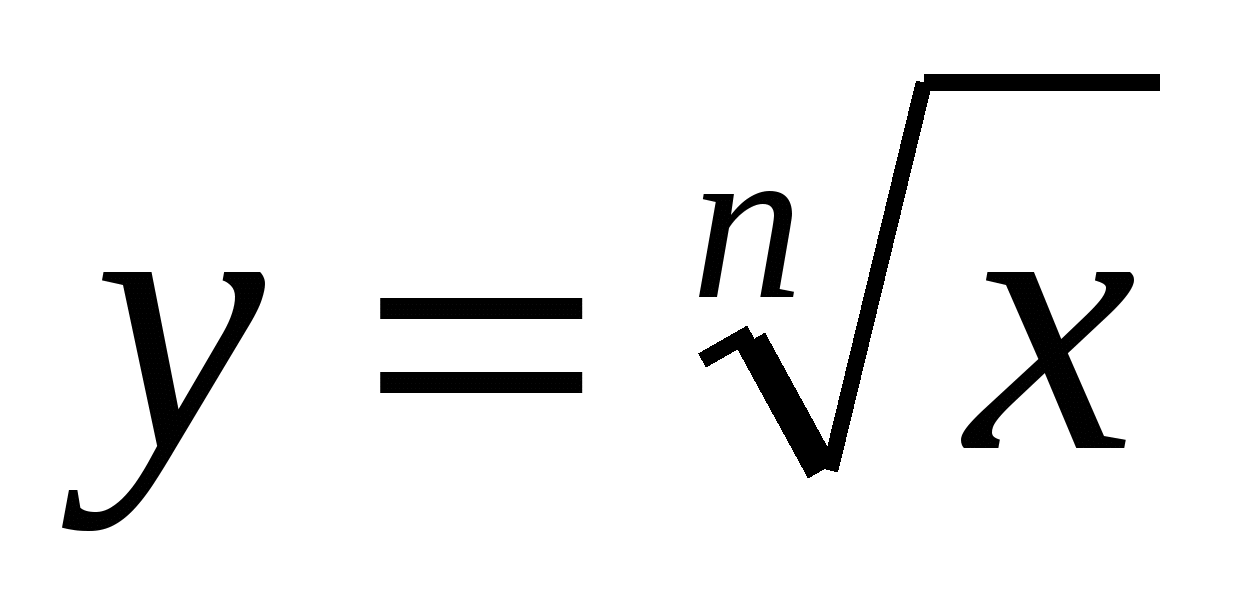 . .
- свойства степенных функций.
- определение степени с рациональным показателем.
Уметь:
- находить значение степени с рациональным показателем;
- проводить преобразования числовых и буквенных выражений, содержащих степени; - строить графики степенных функций, выполнять преобразования графиков;
- находить значение корня натуральной степени;
- проводить преобразования числовых и буквенных выражений, содержащих радикалы;
- пользоваться оценкой и прикидкой при практических расчетах;
- строить графики функции 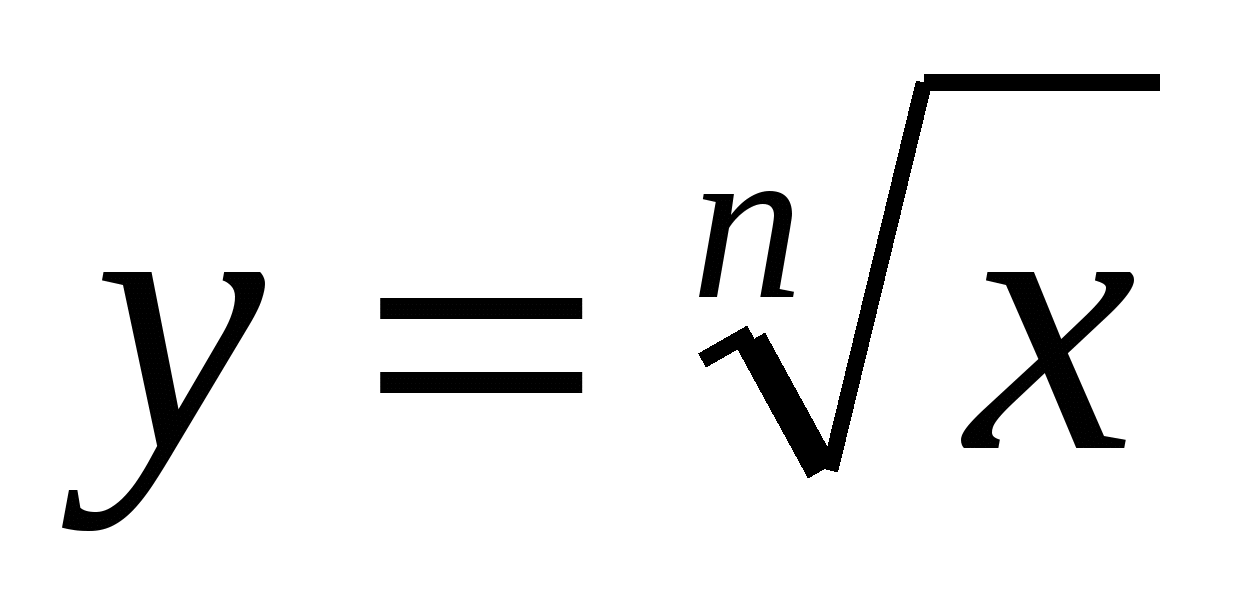 , выполнять преобразования графиков; , выполнять преобразования графиков;
- решать уравнения и неравенства, используя свойства функции 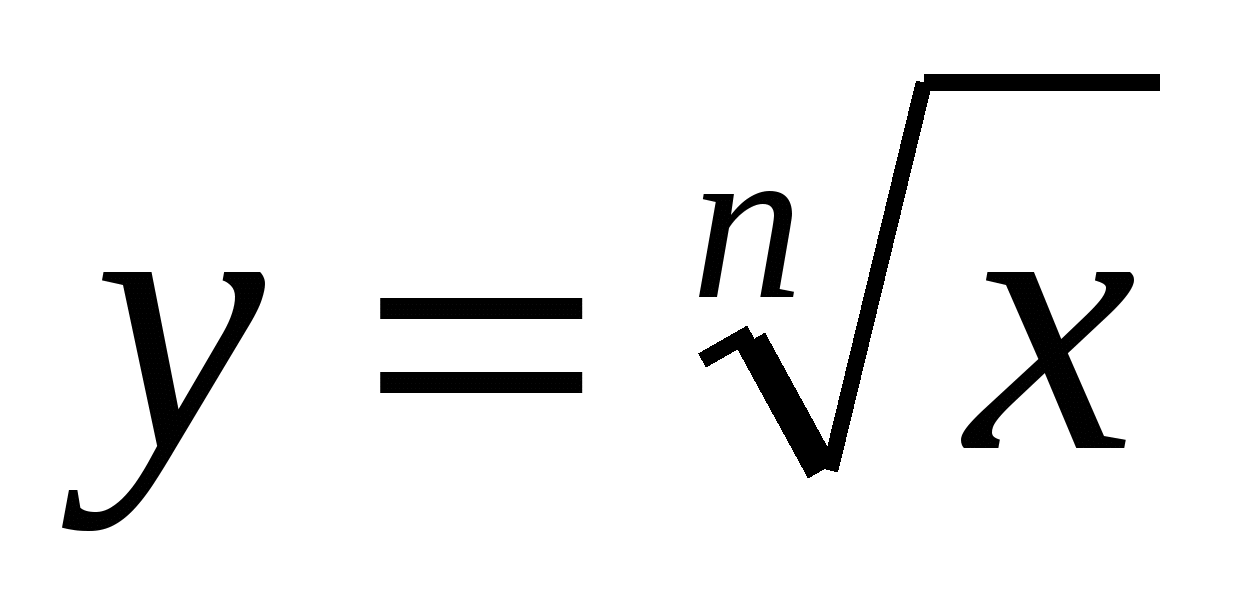 и ее графическое представление. и ее графическое представление.
- описывать по графику и формуле свойства степенной функции;
- решать уравнения и неравенства, используя свойства степенных функции и их графическое представление.
Показательная и логарифмическая функция – 29 ч
Определение показательной функции. Свойства показательной функции в зависимости от основания. Решение показательных уравнений и неравенств, используя график.
Методы решения показательных уравнений. Способы решения показательных неравенств. Определение логарифма. Нахождение значений логарифмов по определению.
Определение логарифмической функции. Зависимость свойств логарифмической функции от основания логарифма. Построение графиков логарифмической функции, решение логарифмических уравнений и неравенств с помощью графиков.
Способы решения логарифмических уравнений. Способы решения логарифмических неравенств. Число е. Функция 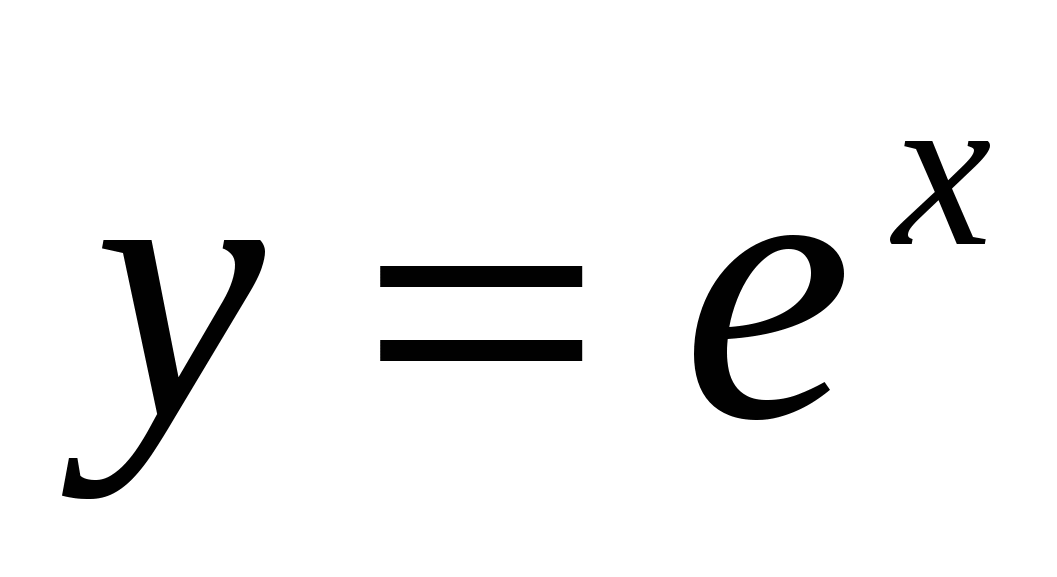 , ее свойства, график, дифференцирование. Натуральные логарифмы. Формулы производных показательной и логарифмической функций. , ее свойства, график, дифференцирование. Натуральные логарифмы. Формулы производных показательной и логарифмической функций.
Контрольная работа №7 по теме «»Показательная и логарифмическая функции»
Контрольная работа №8 по теме «»Логарифмические уравнения и неравенства»
Знать:
- определение показательной функции; определение логарифма; определение натурального логарифма;
- свойства показательной функции; свойства логарифмической функции;
- способы решения показательных уравнений и неравенств; способы решения логарифмических уравнений и неравенств;
- формулы производных показательной и логарифмической функций.
Уметь:
- находить значение логарифмов;
- строить графики логарифмической и показательной функций, выполнять преобразования графиков;
- описывать по графику и формуле свойства логарифмической и показательной функций;
- решать уравнения и неравенства, используя свойства показательных и логарифмических функции и их графическое представление;
- решать показательные и логарифмические уравнения и неравенства и их системы.
- проводить преобразования выражений, содержащих логарифмы;
- вычислять производные показательной и логарифмической функций.
Уравнения и неравенства. Системы уравнений и неравенств – 24 ч
Теоремы а равносильности уравнений. Преобразование данного уравнения в уравнение – следствие. Проверка корней. Потеря корней. Способы решения систем уравнений. Теоремы о равносильности неравенств. Системы и совокупности неравенств.
Способы решения уравнений и неравенств с модулем. Иррациональные уравнения. Иррациональные неравенства. Замена уравнения 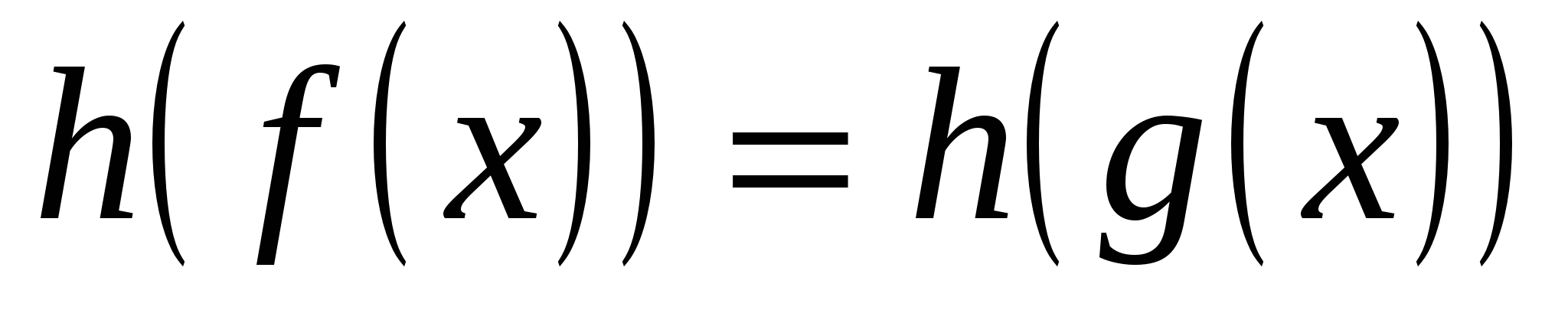 уравнением уравнением 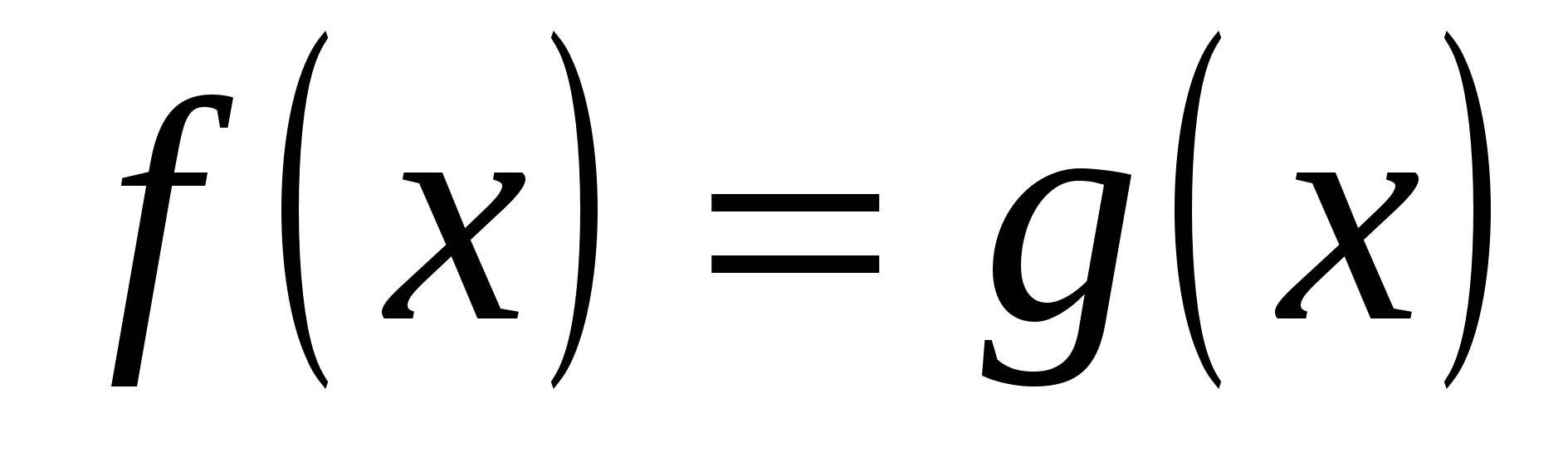 . Метод разложения на множители. Метод введения новой переменной. Функционально-графический метод. . Метод разложения на множители. Метод введения новой переменной. Функционально-графический метод.
Контрольная работа №11 по теме «»Уравнения и неравенства с одной переменной»
Знать:
- определение равносильности уравнений и неравенств;
- способы решения уравнений и систем уравнений;
- понятия системы и совокупности неравенств.
Уметь:
-решать уравнения, неравенства и системы с применением графических представлений и свойств функций;
- доказывать несложные неравенства;
- изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Теория вероятности – 10 ч
Знать:
понятия перестановки, сочетания и размещения
Уметь:
решать простейшие комбинаторные задачи методом перебора, а так же с использованием известных формул
использовать приобретенные знания и умения в практической деятельности для:
анализа реальных числовых данных представленных в виде диаграмм, графиков
анализа информации статистического характера
ГЕОМЕТРИЯ
1. Метод координат в пространстве (15 часов)
Прямоугольная система координат в пространстве. Координаты вектора. Связь между координатами вектора и координатами точек. Простейшие задачи в координатах. Угол между векторами. Вычисление углов между прямыми и плоскостями. Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.
Контрольная работа № 2 по теме «Декартова система координат»
Контрольная работа № 3 по теме «Движение»
Знать:
понятие прямоугольной системы координат в пространстве;
понятие координат вектора в прямоугольной системе координат;
понятие радиус-вектора произвольной точки пространства;
формулы координат середины отрезка, длины вектора через его координаты, расстояние между двумя точками;
понятие угла между векторами;
понятие скалярного произведения векторов;
формулу скалярного произведения в координатах;
свойства скалярного произведения;
понятие движения пространства и основные виды движения.
Уметь:
строить точки в прямоугольной системе координат по заданным её координатам и находить координаты точки в заданной системе координат;
выполнять действия над векторами с заданными координатами;
решать простейшие задачи в координатах;
вычислять скалярное произведение векторов и находить угол между векторами по их координатам;
вычислять углы между прямыми и плоскостям.
2. Цилиндр, конус и шар (17 часов)
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усечённый конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости Касательная плоскость к сфере. Площадь сферы.
Контрольная работа № 6 по теме «Цилиндр, конус, шар»
Знать:
понятие цилиндрической поверхности, цилиндра и его элементов (боковая поверхность, основания, образующие, ось, высота, радиус;
формулы для вычисления площадей боковой и полной поверхностей цилиндра;
понятие конической поверхности, конуса и его элементов (боковая поверхность, основание, вершина, образующая, ось, высота), усечённого конуса;
формулы для вычисления площадей боковой и полной поверхностей конуса и усечённого конуса;
понятия сферы, шара и их элементов(центр, радиус, диаметр);
уравнение сферы в заданной прямоугольной системе координат;
взаимное расположение сферы и плоскости; формулу площади сферы.
Уметь:
решать задачи на вычисление боковой и полной поверхностей цилиндра;
решать задачи на вычисление боковой и полной поверхностей конуса и усечённого конуса;
решать задачи на вычисление площади сферы.
3. Объёмы тел (22 часа)
Понятие объёма. Объём прямоугольного параллелепипеда. Объём прямой призмы. Объём цилиндра. Вычисление объёмов тел с помощью определенного интеграла. Объём наклонной призмы. Объём пирамиды. Объём конуса. Объём шара. Объём шарового сегмента, шарового слоя и шарового сектора. Площадь сферы.
Контрольная работа № 9 по теме «Объемы тел»
Контрольная работа № 10 по теме «Объем шара и площадь сферы»
Знать:
понятие объёма, основные свойства объёма;
формулы нахождения объёмов призмы, в основании которой прямоугольный треугольник и прямоугольного параллелепипеда;
правило нахождения прямой призмы;
что такое призма, вписана и призма описана около цилиндра;
формулу для вычисления объёма цилиндра;
способ вычисления объёмов тел с помощью определённого интеграла, основную формулу для вычисления объёмов тел;
формулу нахождения объёма наклонной призмы;
формулы вычисления объёма пирамиды и усечённой пирамиды;
формулы вычисления объёмов конуса и усечённого конуса;
формулу объёма шара;
определения шарового слоя, шарового сегмента, шарового сектора, формулы для вычисления их объёмов;
формулу площади сферы.
Уметь:
объяснять, что такое объём тела, перечислять его свойства и применять эти свойства в несложных ситуациях;
применять формулы нахождения объёмов призмы при решении задач;
решать задачи на вычисления объёма цилиндра;
воспроизводить способ вычисления объёмов тел с помощью определённого интеграла;
применять формулу нахождения объёма наклонной призмы при решении задач;
решать задачи на вычисление объёмов пирамиды и усечённой пирамиды;
применять формулы вычисления объёмов конуса и усечённого конуса при решении задач;
применять формулу объёма шара при решении задач;
различать шаровой слой, сектор, сегмент и применять формулы для вычисления их объёмов в несложных задачах;
применять формулу площади сферы при решении задач.
Резерв.
Обобщающее повторение. Решение задач (22 часов)
Знать:
основные определения и формулы изученные в курсе геометрии и алгебры
Уметь:
применять формулы при решении задач
использовать приобретенные знания и умения в практической деятельности для решения задач разного уровня сложности на основе изученного материала.
использовать приобретенные знания и умения в практической деятельности для решения задач на основе изученных формул и свойств фигур.
решать текстовые задачи всех видов.
Учебно-тематический план
№
|
Название раздела
|
Количество часов
|
В том числе:
|
уроков
|
к/р
|
|
Повторение материала 10 класса
|
|
7
|
7
|
-
|
1
|
Первообразная и интеграл
|
а
|
9
|
8
|
1
|
2
|
Метод координат в пространстве
|
г
|
15
|
13
|
2
|
3
|
Степени и корни. Степенные функции
|
а
|
20
|
18
|
2
|
4
|
Цилиндр, конус и шар
|
г
|
17
|
16
|
1
|
5
|
Показательная и логарифмическая функция
|
а
|
29
|
27
|
2
|
6
|
Объемы тел
|
г
|
22
|
20
|
2
|
7
|
Уравнения и неравенства. Системы уравнений и неравенств
|
а
|
24
|
22
|
1 к.р-2 часа
|
8
|
Элементы логики, комбинаторики, статистики и теории вероятностей
|
|
10
|
10
|
-
|
9
|
Резерв
|
|
22
|
22
|
-
|
ИТОГО
|
175
|
163
|
12
| |
|
|
 Скачать 0.97 Mb.
Скачать 0.97 Mb.