Административная контрольная работа. Цели

Название	Административная контрольная работа. Цели
Дата	13.04.2016
Размер	55.58 Kb.
Тип	Документы

Административная контрольная работа. Цели
Ответ: 1 2
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №10 станицы Губской муниципального образования Мостовский район
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №10 станицы Губской муниципального образования Мостовский район
Значение дроби меньше соответствующего значения дроби ? Решите систему неравенств
1. Решите неравенство
23. 09. вычитание дробей с разными знаменателями
Решение задач
25. 09. вычитания дробей с разными знаменателями самостоятельная работа
Решение задач
05. 10. деление дробей. Цель
11. 09. основное свойство дроби сокращение дробей самостоятельная работа
Решение задач
05. 09. основное свойство дроби
02. 09. 13 г рациональная дробь
Решение задач

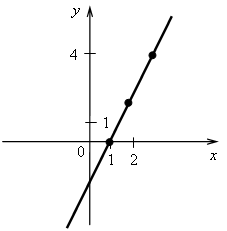
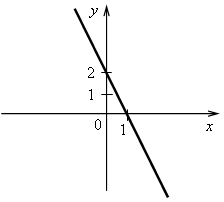
01.10.

административная контрольная работа.

Цели: проверить уровень усвоения знаний и умений по пройденным темам; развивать логическое мышление и вычислительные навыки учащихся; воспитывать внимание и наблюдательность.

Оборудование: карточки с вариантами.

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по двум вариантам.

Вариант 1

1. Упростите выражение (a + 6)² – 2a (3 – 2a).

2. Решите систему уравнений

3. а) Постройте график функции y = 3x – 2.

б) Определите, проходит ли график функции через точку А (–10; –32).

4. Разложите на множители:

а) 2a⁴b³ – 2a³b⁴ + 6a²b²; б) x² – 3x – 3y – y².

5. Из пунктаА вниз по реке отправился плот. Через 1 ч навстречу ему из пунктаВ, находящегося в 30 км от А, вышла моторная лодка, которая встретилась с плотом через 2 ч после своего выхода. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.

Вариант 2

1. Упростите выражение (x – 2)² – (x – 1) (x + 2).

2. Решите систему уравнений

3. а) Постройте график функции y = –2x + 1.

б) Определите, проходит ли график функции через точкуА(10; –19).

4. Разложите на множители:

а) 3x³y³ + 3x²y⁴ – 6xy²; б) 2a + a² – b² – 2b.

5. Из поселка на станцию, расстояние между которыми 32 км, выехал велосипедист. Через 0,5 ч навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.

Решение заданий контрольной работы

Вариант 1

1. (a + 6)² – 2a (3 – 2a) = a² + 12a + 36 – 6a + 4a² = 5a² + 6a + 36.

2.

5х – 2 (4х – 4) = 11;

5х – 8х + 8 = 11;

–3х = 3;

х = –1;

у = 4 · (–1) – 4;

у = –8.

Ответ: (–1; –8).

3. а) График функции y = 2x – 2:

б) А (–10; –20):

–20 = 2 · (–10) – 2;

–20 = –22 – неверно.

Ответ: не проходит.

4. а) 2a⁴b³ – 2a³b⁴ + 6a²b² = 2a²b² (a²b – ab² + 3);

б) x² – 3x – 3y – y² = (x² – y²) – (3x + 3y) = (x – y) (x + y) – 3 (x + y) = (x + y) (x – y – 3).

5. Пусть собственная скорость лодки х км/ч. Выделим процессы: движение плота из пунктаА до встречи с лодкой и движение лодки из пункта В до встречи с плотом.

Заполним таблицу:

	s	υ	t
плот	6 км	2 км/ч	3 ч
лодка	2 (х – 2) км	(х – 2) км/ч	2 ч

Составим и решим уравнение:

6 + 2 (х – 2) = 30;

6 + 2х – 4 = 30;

2х = 28;

х = 14.

Ответ: 14 км/ч.

Вариант 2

1. (x – 2)² – (x – 1) (x + 2) = x² – 4x + 4 – x² – 2x + x + 2 = –5x + 6.

2.

3 (2у – 7) + 5у = 12;

6у – 21 + 5у = 12;

11у = 33;

у = 3;

х = 2 · 3 – 7;

х = –1.

Ответ: (–1; 3).

3. а) График функции y = –2x + 2:

б) А (10; –18):

–18 = –2 · 10 + 2;

–18 = –18 – верно.

Ответ: проходит.

4. а) 3x³y³ + 3x²y⁴ – 6xy² = 3xy² (x²y + xy² – 2);

б) 2a + a² – b² – 2b = (2a – 2b) + (a² – b²) = 2 (a – b) + (a – b) (a + b) = (a – b) (2 + a + b).

5. Пусть скорость велосипедиста х км/ч, тогда скорость мотоциклиста (х + 28) км/ч. Выделим процессы: движение велосипедиста до встречи с мотоциклистом и движение мотоциклиста до встречи с велосипедистом.

Заполним таблицу:

	s	υ	t
велосипедист	х км	х км/ч	1 ч
мотоциклист	0,5 (х + 28) км	(х + 28) км/ч	0,5 ч

Составим и решим уравнение:

х + 0,5 (х + 28) = 32;

х + 0,5х + 14 = 32;

1,5х = 18;

х = 12.

Получаем, что скорость велосипедиста равна 12 км/ч, тогда скорость мотоциклиста равна 12 + 28 = 40 км/ч.

Ответ: 12 км/ч и 40 км/ч.
III. Итоги урока.
IV. Домашнее задание: повторить основные правила и подготовиться к устному опросу.