Протокол № от 20 г. Согласовано зам. Директора Анисимова Ю. В. Утверждаю директор
 Скачать 471.47 Kb.
|
| МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ЛОКТЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
Рабочая программа учебного предмета основного общего образования «Алгебра» в 8 классе на 2015-2016 учебный год Составитель: Сафронова Л.Н. учитель математики I квалификационной категории с..Локоть 2015 Пояснительная записка Рабочая программа учебного курса по алгебре для 8 класса разработана на основе:
Место предмета в федеральном базисном учебном плане Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится 5,5ч в неделю в 8 классах. Из них на алгебру - 4 часа в неделю в I полугодии и 3 ч в неделю во II полугодии, всего 119ч и геометрию 68 часов – 2 часа в неделю. Учебный год для учащихся 8 классов состоит из 35 учебных недель, в связи с этим добавлено3 ч. Итого рабочая программа по алгебре рассчитана на 122 ч. Общая характеристика предмета Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов, явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. Формы контроля: текущий контроль, промежуточный контроль, итоговый контроль В процессе обучения используются групповые формы работы, работа в парах, индивидуальная работа, фронтальная работа. Методы: проблемный, частично-поисковый, репродуктивный, исследовательский. Предусмотрено 10 контрольных работ, итоговый зачёт - 1. Изучение алгебры в 8 классе направлено на достижение следующих целей:
При реализации рабочей программы используется дополнительный материал в ознакомительном плане - «Раздел для тех, кто хочет знать больше», создавая условия для максимального математического развития учащихся, интересующихся предметом, для совершенствования возможностей и способностей каждого ученика. Выявление итоговых результатов изучения темы завершается контрольной работой. Контрольные работы составляются с учетом обязательных результатов обучения. В целях усиления развивающих функций задач, развития творческой активности учащихся, активизации поисково-познавательной деятельности используются творческие задания, задачи на моделирование, задания практического характера. В целях развития межпредметных связей, усиления практической направленности предмета включены задачи физического характера, задачи из химии, биологии. Результаты обучения. Результаты обучения представлены в требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика. Содержание 1. Рациональные дроби Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Преобразование рациональных выражений. Функция  и её график.Цель – выработать умение выполнять тождественные преобразования рациональных выражений. Знать основное свойство дроби, рациональные, целые, дробные выражения; правильно употреблять термины «выражение», «тождественное преобразование», понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь. Знатьи понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь, свойства обратной пропорциональности Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия сложения и вычитания с алгебраическими дробями, сокращать дробь, выполнять разложение многочлена на множители применением формул сокращенного умножения, выполнять преобразование рациональных выражений. Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия умножения и деления с алгебраическими дробями, возводить дробь в степень, выполнять преобразование рациональных выражений; правильно употреблять функциональную терминологию (значение функции, аргумент, график функции), строить график обратной пропорциональности, находить значения функции y=k/x по графику, по формуле. 2. Квадратные корни Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближённое значение квадратного корня. Свойства квадратных корней. преобразования выражений, содержащих квадратные корни. Функция 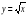 и её график.Цель – систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни. Знатьопределения квадратного корня, арифметического квадратного корня, какие числа называются рациональными, иррациональными, как обозначается множество рациональных чисел; свойства арифметического квадратного корня. Уметь выполнять преобразование числовых выражений, содержащих квадратные корни; решать уравнения вида x2=а; находить приближенные значения квадратного корня; находить квадратный корень из произведения, дроби, степени, строить график функци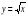и  и находить значения этой функции по графику или по формуле; выносить множитель из-под знака корня, вносить множитель под знак корня; выполнять преобразование выражений, содержащих квадратные корни.3. Квадратные уравнения Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям. Цель – выработать умения решать квадратные уравнения, простейшие рациональные уравнения и применять из к решению задач. Знать, что такое квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения, терему Виета и обратную ей. Уметь решать квадратные уравнения выделением квадрата двучлена, решать квадратные уравнения по формуле, решать неполные квадратные уравнения, решать квадратные уравнения с помощью теоремы, обратной теореме Виета, использовать теорему Виета для нахождения коэффициентов и свободного члена квадратного уравнения; решать текстовые задачи с помощью квадратных уравнений. Знатькакие уравнения называются дробно-рациональными, какие бывают способы решения уравнений, понимать, что уравнение – это математический аппарат решения разнообразных задач математики, смежных областей знаний, практики. Уметьрешать дробно-рациональные уравнения, решать уравнения графическим способом, решать текстовые задачи с помощью дробно-рациональных уравнений. 4. Неравенства Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной. Цель – выработать умения решать линейные неравенства с одной переменной и их системы. Знатьопределение числового неравенства с одной переменной, что называется решением неравенства с одной переменной, что значит решить неравенство, свойства числовых неравенств, понимать формулировку задачи «решить неравенство». Уметьзаписывать и читать числовые промежутки, изображать их на числовой прямой, решать линейные неравенства с одной переменной, решать системы неравенств с одной переменной. Уметьприменять свойства неравенства при решении неравенств и их систем. 5. Степень с целым показателем Степень с целым показателем и её свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями. Цель – сформировать умение выполнять действия над степенями с целыми показателями, ввести понятие стандартного вида числа. Знать определение степени с целым и целым отрицательным показателем; свойства степени с целым показателями. Уметьвыполнять действия со степенями с натуральным и целым показателями; записывать числа в стандартном виде, записывать приближенные значения чисел, выполнять действия над приближенными значениями. 6. Элементы статистики и теории вероятностей Сбор и группировка статистических данных. Наглядное представление статистической информации 7. Повторение. Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 8 класса). Структура изучаемого предмета
| ||||||||||||||||||||||||||||||||||||||||||||||