Тест 1 Диагностика пробелов знаний
 Скачать 73.69 Kb. Скачать 73.69 Kb.
|
Тест 1 Диагностика пробелов знаний Вариант 1 А1. Найдите значение выражения 1) 16; 2) 12; 3) 6; 4) 24. А2. Найдите значение выражения 1) 0; 2) 1,2; 3) 2; 4) –1,2. А3. Укажите значение выражения log484 + log4(21)-1. 1) log43; 2) 1; 3) 2; 4) 0. A4. Вычислите sin(-6900). 1) А5. Найдите сумму корней уравнения х3 –3х2 -4х +12 = 0. 1) -3; 2) 7; 3) -7; 4) 3. А6. Найдите корни уравнения 1) –8 и 3; 2) -3 и 8; 3) -3; 4)8. А7. Укажите промежуток, которому принадлежит корень уравнения 5х ·5х+5 = 1. 1) [-4;-2]; 2) (-2;0); 3) [0;2]; 4) (2;4). A8. Укажите промежуток, которому принадлежит корень уравнения log2(х –1)3=6 1) (0;6); 2) [-6;0); 3) [18;26]; 4) (26; 30). А9.Найдите сумму корней уравнения х2-4х+|x -3|+3= 0. 1) 3; 2) 2; 3) 5; 4) -1. А10. При каком значении параметра а уравнение ах2 – х+3=0 имеет один корень? 1) А11. Сколько корней имеет уравнение 1) 1; 2) 2; 3) 3; 4) ни одного. А12. Пусть (хо; уо) - решение системы уравнений 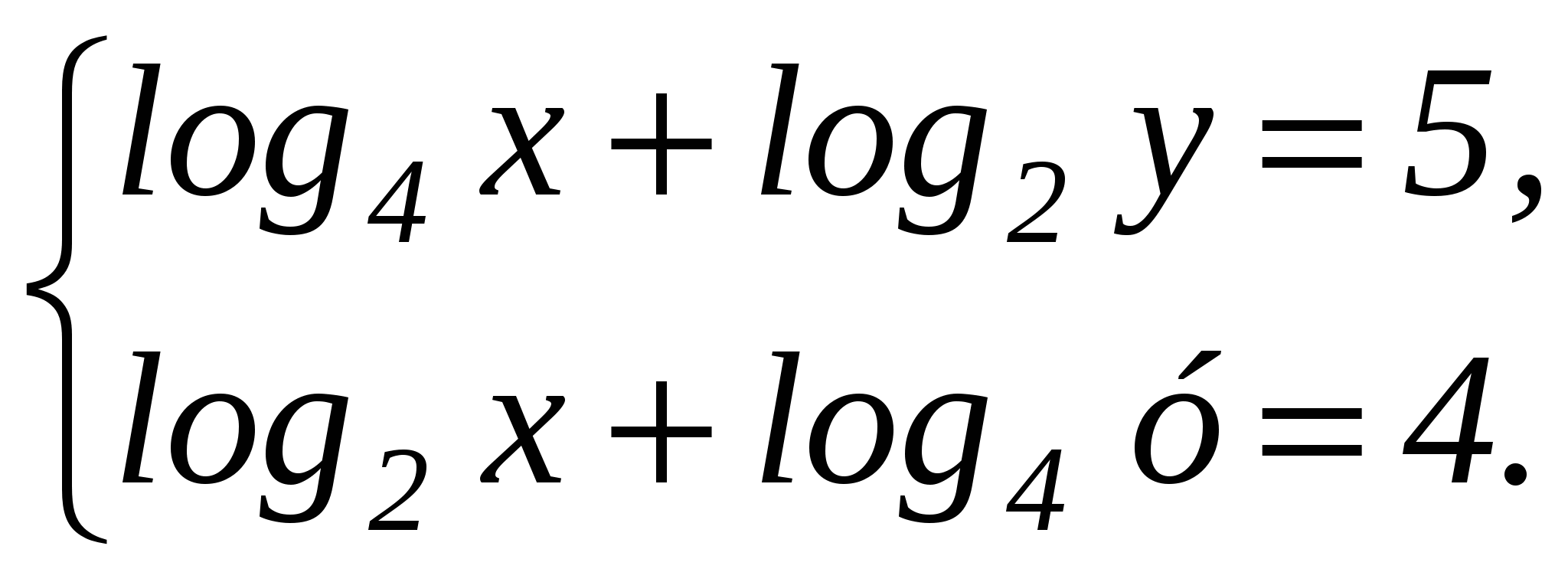 Найдите разность хо- уо. 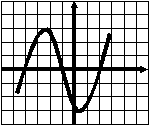 1) 8; 2) -12; 3) -8; 4) 12. 1) 8; 2) -12; 3) -8; 4) 12. А13. На рисунке изображен график функции у =f(x) у Укажите сумму корней уравнения f(x)= 0. 1 у=f(x) 0 1 х 1) 3; 2) -4; 3) -5; 4) -3. А14. Решите неравенство 1) (-¥;-3]È(0;4); 2) (-3;0)È(4; +¥); 3) [-3;0]È[4; +¥); 4) [-3;0)È(4; +¥). А15. Укажите наименьшее целое решение неравенства 1) 0; 2) 2; 3) 10; 4) 9. А16. Решите неравенство 1) (-¥; 0); 2) (0; +¥); 3) (-¥;-4]; 4) [-4; +¥). А17. Найдите число целых решений неравенства log5 (5 –2x) < 1. 1) 2; 2) 3; 3) 1; 4) 4. А18. На каком графике изображена функция у= 2-х ? 1   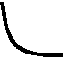 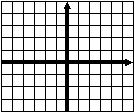 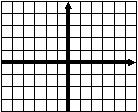 ) у 2) у 3) у 4) у ) у 2) у 3) у 4) у 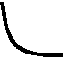   1 1 1 1 1 1 1 10 1 х 0 1 х 0 1 х 0 1 х А19. Найдите область определения функции f(x)= 1) (-¥; 1)È(1; +¥); 2) [1; +¥); 3) (-¥;1]; 4) [0;1]. А20. Найдите область значений функции 1)(0;+); 2) (-; +); 3) [4; 2]; 4) [4; +). А21. Укажите рисунок, на котором изображен график нечетной функции. 1   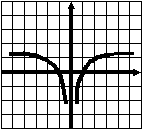 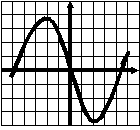 ) y 2) y 3) y 4) y ) y 2) y 3) y 4) y 1 1 1 1 0 1 x 0 1 x 0 1 x 0 1 x А 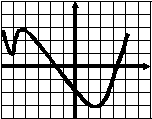 22.Функция задана на промежутке [-6;4] (см. рисунок). у 22.Функция задана на промежутке [-6;4] (см. рисунок). уУкажите промежуток, на котором функция не убывает. 1 1) [-5;-3]; 2) [2;3]; 3) [0;4]; 4)[1;2]. 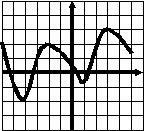 у уА23. Функция у=f(x) задана на промежутке [-6;5]. Найдите наименьший промежуток, которому 1 1 принадлежат все точки экстремумов функции. 0 х 1) [-5;3]; 2) [-6;5]; 3) [-4;3]; 4)[-5;5]. 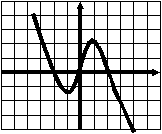 А24. На рисунке изображен график функции у =f(x). у Пользуясь графиком, найдите все значения аргумента, при которых функция принимает 1 отрицательные значения . 0 1 х 1) (2;+); 2) (-;-2)È (0;2); 3) (-2;0)È (2;+); 4) (-2;0). Тест 1. Диагностика пробелов знаний Вариант 2 А1. Найдите наименьшее из нижеприведенных чисел, 0 < m < 1 . 1) А2. Найдите наименьшее из нижеприведенных чисел. 1) (-0,2)4; 2) (-0,2)3; 3) (-0,2)5; 4) (-0,2)-6. А3. Найдите значение выражения: log 1) kp; 2) А4. Упростите выражение 1) 1; 2) -100; 3) 100; 4) -10. А5. При каких значениях с уравнение сх2+2х+1=0 имеет два корня ? 1) [-1;1]; 2) (-¥; 0)È(0; -1); 3) (-¥; -1); 4) (-¥; 1). А6. Найдите корни уравнения 1) 3; 2) -3 и 8; 3) -3; 4)8. А7. Укажите промежуток, содержащий все корни уравнения 1) (-¥; -1); 2) (-2; +¥); 3) [-2; -1] 4) нет действительных корней. А8. Какому промежутку принадлежит произведение всех различных корней уравнения log2(x+3)=log25x+log27 ? 1) (-¥; -0,5); 2) [-0,5; 0,5); 3) [0,5; e); 4) [e; +¥). А9. Найдите сумму корней уравнения |x-3| - |x+8| =5. 1) -5; 2) 0; 3) 8; 4) 5. А10. Назовите наибольшее целое положительное значение параметра а, при котором уравнение 4 х2 – ах +1=0 не имеет корней. 1) 1; 2) 4; 3) 15; 4) 3. А11. Укажите число корней уравнения 1) 1; 2) 2; 3) 3; 4) ни одного. А12. Пусть (хо; уо) - решение системы уравнений 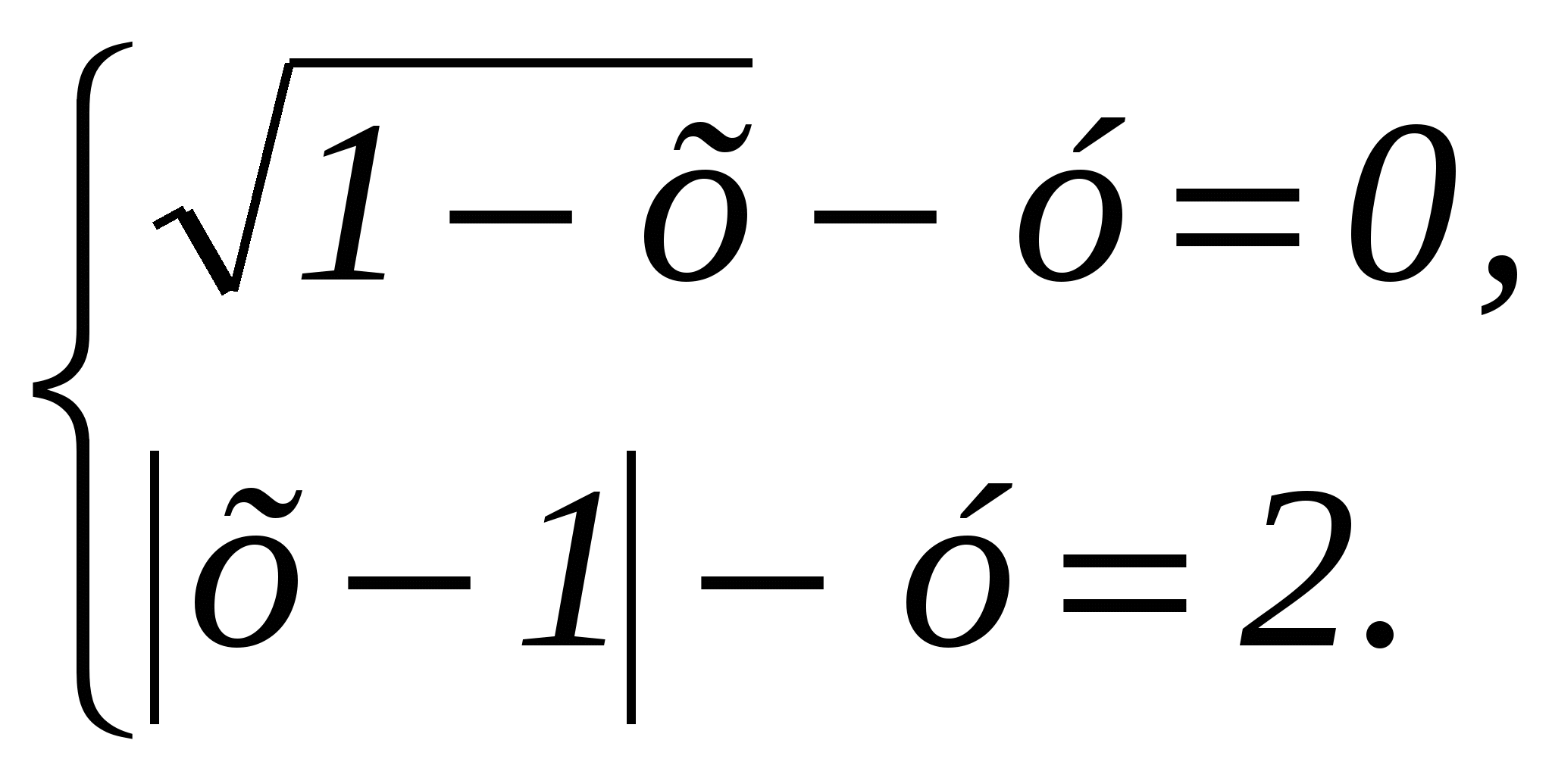 Найдите разность хо- уо. 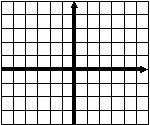 1) 5; 2) 3; 3) -5; 4) -1. 1) 5; 2) 3; 3) -5; 4) -1. А 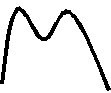 13. На рисунке изображен график функции у =f(x) у 13. На рисунке изображен график функции у =f(x) у Укажите больший корень уравнения f(x)= 0. у=f(x) 1 0 1 х 1) 0; 2) 4; 3) 5; 4) -3. А14.Укажите множество решений неравенства 1) (-3;-2]È[8;+¥); 2) (-3;2)È(8; +¥); 3) [-3;-2]È[8; +¥); 4) [-3;-2)È(8; +¥). А15.Укажите наименьшее целое решение неравенства 1) 3; 2) -1; 3) 0; 4) 1. А16.Найдите сумму всех целых решений неравенства 0,3(х+1)(х-5) -1≥ 0. 1) 14; 2) 8; 3)-14; 4) 12. А17.Решите неравенство log0,5(1-0,5x) >-3. 1)(-¥; 2); 2) [-14; 2]; 3) (-14;2); 4) (-14; +¥). А18. На каком графике изображена функция у=х 4? 1 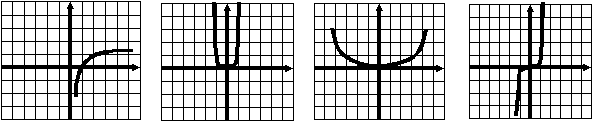 ) 2) 3) 4) ) 2) 3) 4) у у у у 1 1 1 1 0 1 х 0 1 х 0 1 х 0 1 х А19.Найдите область определения функции у =f(x), 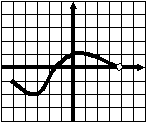 заданной графиком на рисунке. у заданной графиком на рисунке. у 1) [-2; 1]; 2) [-5;4); 3) (-5;4); 4) (-2; 1). 0 1 х А20.Найдите множество значений функции 1)(0;+¥]; 2) А21. Укажите рисунок, на котором изображен график четной функции. 1 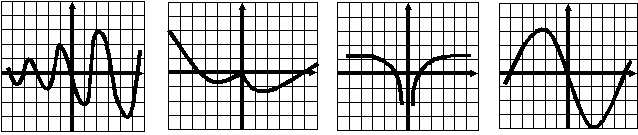 ) y 2) y 3) y 4) y ) y 2) y 3) y 4) y 1 1 1 1 0 1 x 0 1 x 0 1 x 0 1 x А 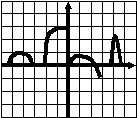    22.Укажите функцию, убывающую на промежутке [-2;0] и возрастающую на промежутке [0;3]: 22.Укажите функцию, убывающую на промежутке [-2;0] и возрастающую на промежутке [0;3]:1) у 2) у 3) у 4) у 1 1 1 0 1 х 0 1 х 0 1 х 0 1 х А23 Найдите наибольшее значение функции у= -2х2+8х -7. 1) -2; 2) 7; 3) 1; 4) 2. А24. Найдите нули функции 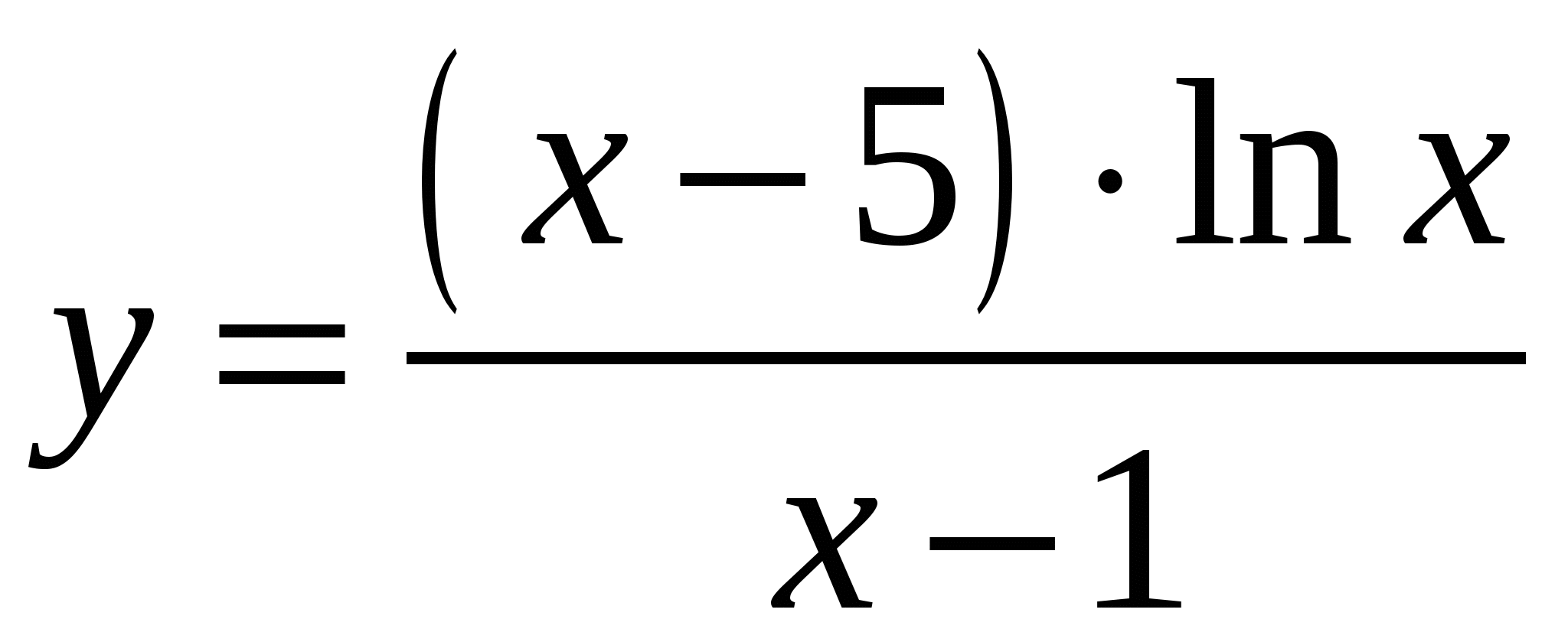 1) 5; 2) 1; 3) 0; 4) 5 и 1. Ответы:
|