| Фото на холсте киев Фото на холсте киев печать фотографий и картин на холсте. artdiscount.com.ua |
Тест 7 Применения производной к исследованию функций
 Скачать 33.54 Kb.
|
Тест 7 Применения производной к исследованию функций Вариант 1 А1. Укажите промежуток, на котором функция  только возрастает.1)  2)  3)  4)  А2. Укажите промежуток, на котором функция 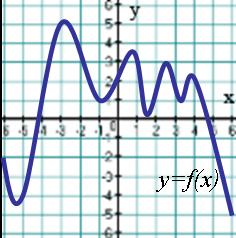 убывает.1  )  2)  3)  4)  А3. На рисунке изображен график функции  . Сколько точек минимума имеет функция?1) 4 2) 5 3) 2 4) 1 А4. Найдите точку максимума функции  .1) -4 2) -2 3) 4 4) 2 А5. Сколько критических точек имеет функция 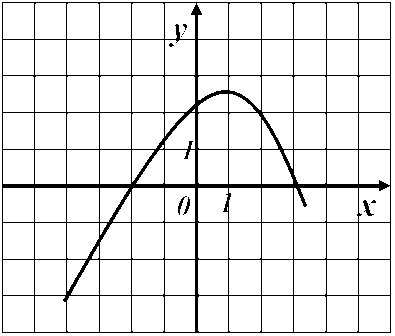 ? 1) 2 2) 1 3) 4 4) 3А6. На рисунке изображен график производной у =f ´(x). Найдите точку максимума функции у =f(x). 1) 1 2) 3 3) 2 4) -2 А7. Найдите точку минимума функции  .1 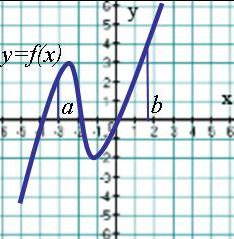 ) -2 2) -0,5 3) 0,5 4) 2А8. График функции у=f(x) изображен на рисунке. Укажите наибольшее значение этой функции на отрезке  1) 2 2) 3 3) 4 4) 6 А9. Найдите наименьшее значение функции  на отрезке  . 1)  2) 3 3) 1 4) -А10. Найдите наименьшее значение функции у=2sin  -1. 1) -1; 2) -3; 3) -2; 4) -  . Тест 7 Применения производной к исследованию функций Вариант 2 А1. Укажите промежуток, на котором функция то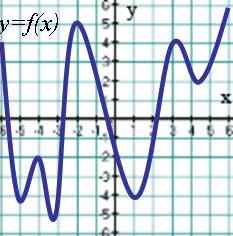лько убывает.1) 2) 3) 4) А  2. Укажите промежуток, на котором функция  возрастает.1)  2) 3)  4)  А3. На рисунке изображен график функции . Сколько точек минимума имеет функция?1) 5 2) 3 3) 2 4) 1 А4. Найдите точку максимума функции  .1) -3 2) -2 3) 3 4) 2 А5. Сколько критических точек имеет функция  ?1) 2 2) 1 3) 4 4) 3А6. На рисунке изображен график производной у =f ´(x). Найдите точку минимума функции у =f(x). 1) 1 2) 3 3) -4 4) -2 А7. Найдите точку максимума функции .1 ) -2 2) -0,5 3) 0,5 4) 2А8. График функции у=f(x) изображен на рисунке. Укажите наименьшее значение этой функции на отрезке 1) 2 2) -2 3) -4 4) 6 А9. Найдите наибольшее значение функции на отрезке . 1) 2) 3 3) 2 4) 4А10. Найдите наибольшее значение функции у=2sin -1. 1) 1 2) 3 3) 2 4) Ответы:
|