Исследование функции по графику ее производной функции у= f ( X ) задана на отрезке [ a ; b
 Скачать 22.81 Kb.
|
Тест 7 Исследование функции по графику ее производной 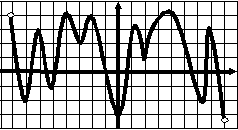 В1. Функции у=f(x) задана на отрезке [a;b]. у На рисунке изображен график ее производной у=f ´(x). Исследуйте на экстремумы 1 b функцию у=f(x). В ответе укажите количество a 0 1 х точек минимума. 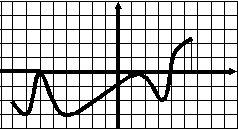 В2. Функции у=f(x) задана на отрезке [a;b]. На рисунке изображен график ее производной у у=f ´(x). Исследуйте функцию у=f(x) на монотонность и в ответе укажите длину 1 промежутка убывания. а 0 1 b х 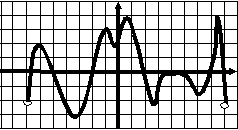 В3. Функции у=f(x) определена на промежутке у (-7; 8). На рисунке изображен график ее производной у=f ´(x). Найдите промежутки -7 1 8 невозрастания функции у=f(x). В ответе 0 1 х укажите наибольшую из длин этих промежутков. 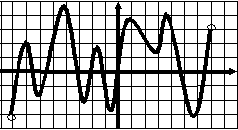 В4. Функции у=f(x) определена на промежутке у (а; b). Ее производной является функция у=f ´(x), а на рисунке изображен график функции a 1 b у=f ´(x)+2. Укажите число точек максимума 0 1 x функции у=f(x) на промежутке (а; b). В 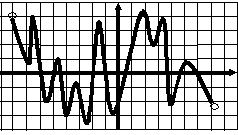 5. Функции у=f(x) определена на промежутке(а; b). На рисунке изображен график ее у производной. Укажите число точек максимума функции у = f(x) - х на промежутке (а; b). a 1 b 0 1 х В 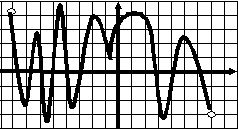 6. Функции у=f(x) определена на промежутке(а; b). На рисунке изображен график ее у производной. Укажите число точек минимума функции у = f(x) - 3х на промежутке (а; b). 1 a 0 1 b х В 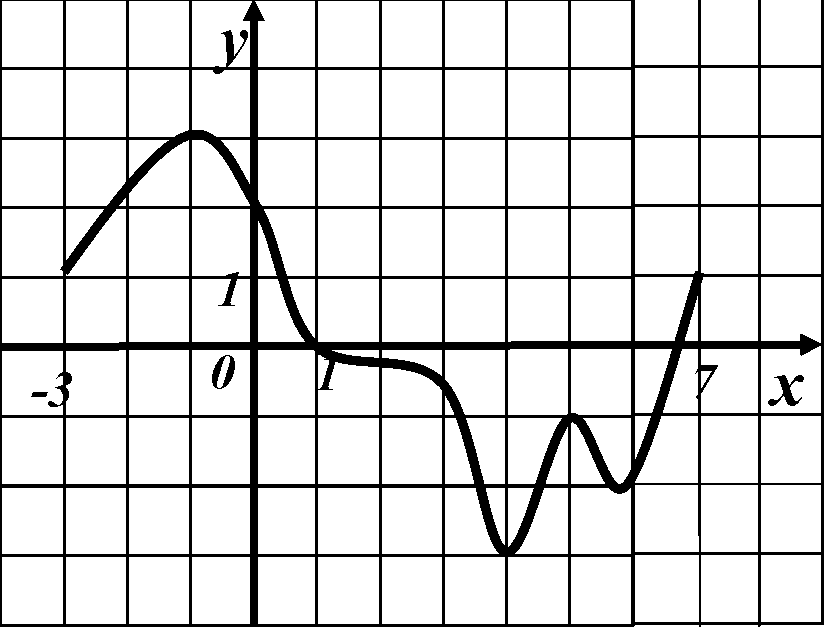 7. Функция  определена на промежутке (– 3; 7). На рисунке изображен график ее производной. Найдите точку 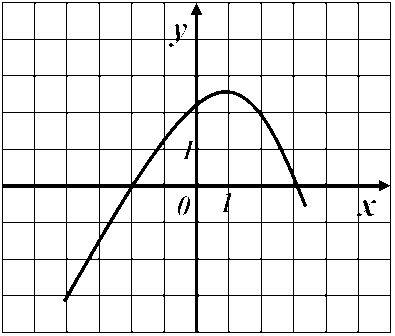 , в которой функция принимает наибольшее значение. В8. На рисунке изображен график производной у =f ´(x). Найдите точку максимума функции у =f(x). 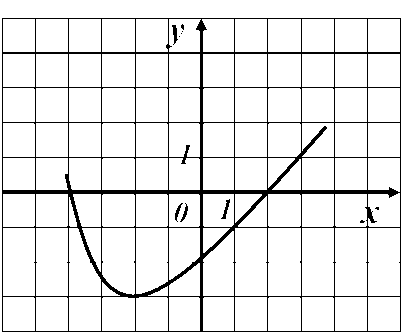 В9. На рисунке изображен график производной у =f ´(x). Найдите точку минимума функции у =f(x). |