Тема Геометрический и физический смысл производной
 Скачать 42.57 Kb.
|
1. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 3 +2x –x2 в его точке с абсциссой х0 = 1. 1) 1; 2) –2; 3) 0; 4) 4. 2. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = x5 –5x2 -3 в его точке с абсциссой х0 = -1. 1) 15; 2) 12; 3) 11; 4) 7. 3. Через точку графика функции у=х3+2loge  с абсциссой хо=2 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс. 1) 11; 2) 12; 3) 13; 4) 14. 4. Через точку графика функции 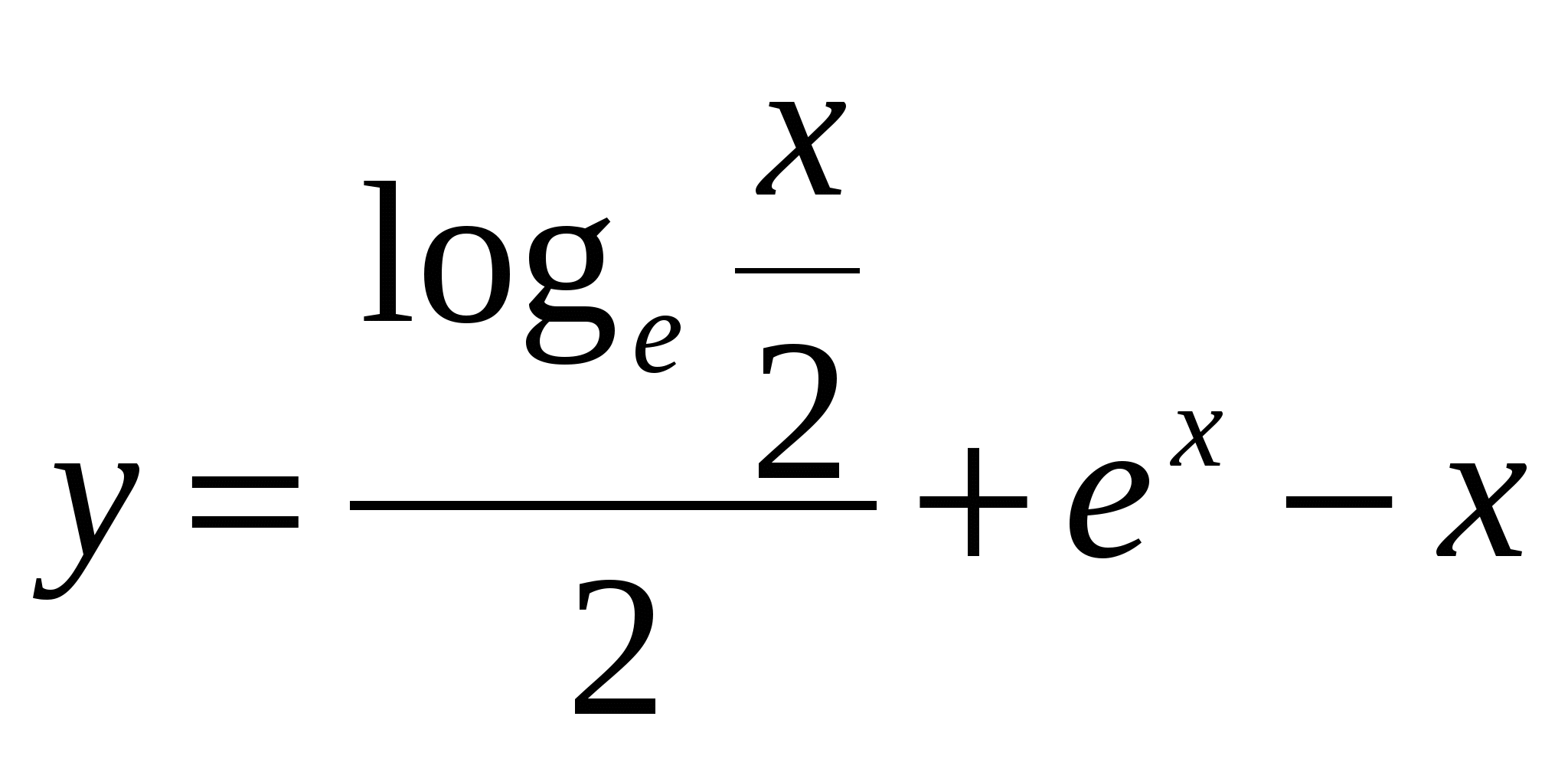 с абсциссой хо=1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс. 1) ех+1; 2) ех -1; 3)  ; 4)е - . 5. Найдите тангенс угла наклона касательной к графику функции f(x)=5x2+3x-1 в точке с абсциссой хо=0,2. 1) 5; 2) -0,2; 3)  ; 4) 53.6. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 9x –4x3 в его точке с абсциссой х0 = 1. 1) -3; 2) 0; 3) 3; 4) 5. 7. Через точку графика функции  с абсциссой хо = -2 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.1) 7; 2) -3; 3) -5; 4) -9 8.Через точку графика функции у= х+ lnx+  с абсциссой хо=2 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.1) 2  ; 2) 1; 3) 1 ; 4) .9.Через точку графика функции у=2ln  +tg(x+2) с абсциссой хо= -2 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.1)  ; 2) -1;; 3) -; 4) 0. 10. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) =  в точке х0 = 0.1) 1; 2) 0; 3) 0,5; 4) –1.  11. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = ex +2x в точке х0 = 0. 1) 3; 2) 0; 3) 2; 4) e +2. 12.При движении тела по прямой расстояние S (в метрах) от начальной точки изменяется по закону S(t)=t3- t2+5t+1 (t –время движения в секундах). Найти скорость (м/с) тела через 3 секунды после начала движения. 1) 26; 2) 24; 3) 16; 4) 30. 13. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = х3 - х4+17x+8 в точке х0 = -3. 1) -151; 2) 152; 3) -64; 4) 52. 14. При движении тела по прямой расстояние (в метрах) от начальной точки изменяется по закону  ( t – время движения в секундах). Через сколько секунд после начала движения тело сделает вторую мгновенную остановку (Vмгн=0) ? 1) 1; 2) 7; 3) 5; 4) 8. 15. При движении тела по прямой расстояние (в метрах) от начальной точки изменяется по закону 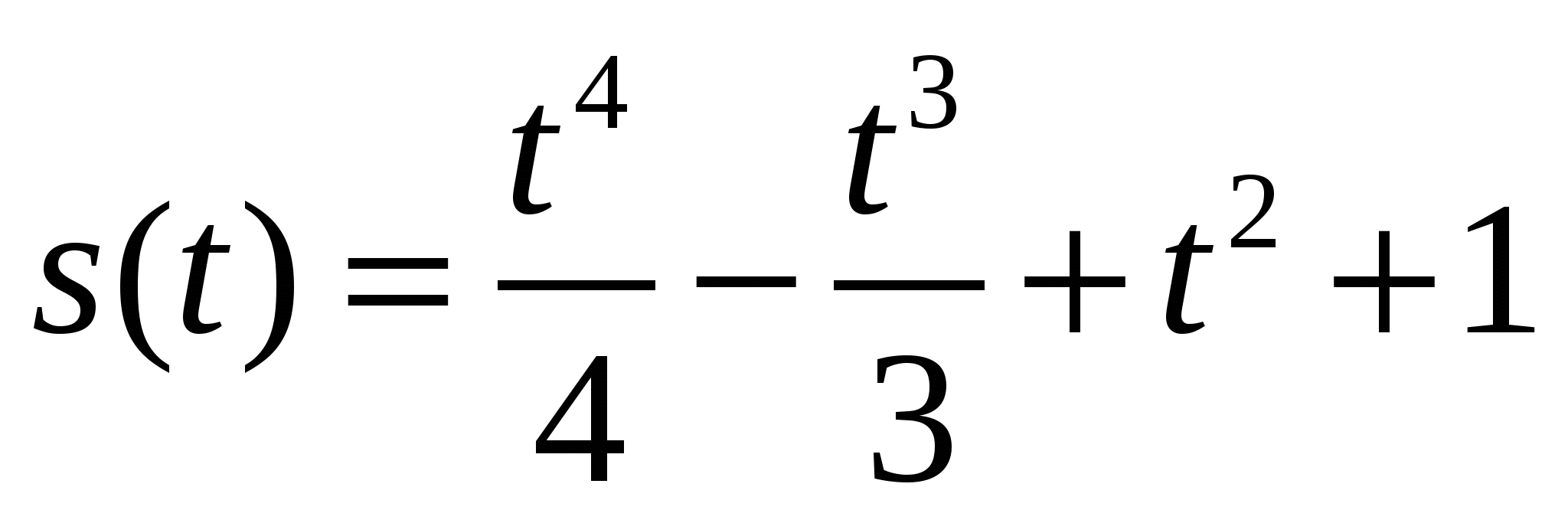 ( t – время движения в секундах). Найти скорость тела (м/с) через 4 секунды после начала движения.1) 18 2) 72 3) 56 4) 48
|