Тест Экстремумы. Наибольшее (наименьшее) значение функции

Скачать 29.19 Kb. Название Тест Экстремумы. Наибольшее (наименьшее) значение функции Дата 11.04.2016 Размер 29.19 Kb. Тип Документы

1. /Тематические тесты/Тест 1 Диагностика пробелов знаний.doc 2. /Тематические тесты/Тест 10 Диагностика пробелов в знаниях.doc 3. /Тематические тесты/Тест 11 Выражения и их преобразования.doc 4. /Тематические тесты/Тест 12 Уравнения.doc 5. /Тематические тесты/Тест 13 Графический метод решения неравенств.doc 6. /Тематические тесты/Тест 14 Общие приемы решения уравнений.doc 8. /Тематические тесты/Тест 16 Понятие функции. Область определения функции..doc 9. /Тематические тесты/Тест 17 Область значений функции.doc 10. /Тематические тесты/Тест 2 Тригонометрические функции.doc 11. /Тематические тесты/Тест 3 Геометрический и физический смысл производной.doc 12. /Тематические тесты/Тест 4 Производная. Правила дифференцирования.doc 13. /Тематические тесты/Тест 5 Исследование функции по графику ее производной.doc 14. /Тематические тесты/Тест 6 Экстремумы. Наибольшее (наименьшее) значение функции.doc 15. /Тематические тесты/Тест 7 Применения производной к исследованию функций.doc 16. /Тематические тесты/Тест 8 Первообразная и интеграл.doc Тест 1 Диагностика пробелов знаний Диагностический тест Тест 11 Выражения и их преобразования Вариант 1 Вычислите. 1 2; 2 3; 3 9; 2 Тест 12 Уравнения Тема Графический метод решения неравенств Тема Общие приемы решения уравнений Тест 16. «Понятие функции. Область определения функции» Тест 17. «Область значений функции» Тест 2 Тригонометрические функции Тема Геометрический и физический смысл производной Тест 4 Производная. Правила дифференцирования Исследование функции по графику ее производной функции у= f ( X ) задана на отрезке [ a ; b Тест Экстремумы. Наибольшее (наименьшее) значение функции Тест 7 Применения производной к исследованию функций Тест 8 Первообразная и интеграл Тест 6. Экстремумы. 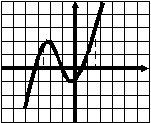Наибольшее (наименьшее) значение функции. Вариант 1. у 1. График функции у=f(x) изображен на рисунке. Укажите наибольшее значение этой функции 1 на отрезке [a;b]. а 0 1 b х 1) 2,5; 2) 3; 3) 4; 4) 2. 2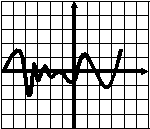. у На рисунке изображен график функции у=f(x). Сколько точек минимума имеет функция? 1 0 1 х 1) 5; 2) 6; 3) 4; 4) 10. 3. В какой точке функция у= -3х2+12х -5 принимает наибольшее значение? 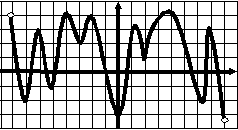1) -4; 2) -2; 3) 4; 4) 2. 4. Функции у=f(x) задана на отрезке [a;b]. у На рисунке изображен график ее производной у=f ´(x). Исследуйте на экстремумы 1 b функцию у=f(x). В ответе укажите количество a 0 1 х точек минимума. 1) 6; 2) 7; 3) 4; 4) 5. 5. Найдите наибольшее значение функции у= -2х2+8х -7. 1) -2; 2) 7; 3) 1; 4) 2. 6. Найдите наименьшее значение функции на отрезке [0;4]. 1) ; 2) 3; 3) 1; 4) -. 7. Найдите наименьшее значение функции у=|2х+3| -. 1) -; 2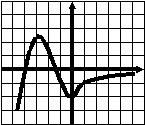) 0; 3) ; 4) -. 8. При каком значении параметра р функция имеет минимум в точке хо=1,5 ? 1) 5; 2) -6; 3) 4; 4) 6. у 9. Укажите наибольшее значение функции у=f(x), график которой изображен на рисунке. 1 х 0 1 1) 2,5; 2) 3; 3) -3; 4) 0. 10. Найдите наибольшее значение функции у=lg(100 –x2). 1) 10; 2) 100; 3) 2; 4) 1. 11. Найдите наименьшее значение функции у=2sin-1. 1) -1; 2) -3; 3) -2; 4) -. Тест 6. Экстремумы. Наибольшее (наименьшее) значение функции. Вариант 2 y 1. График функции у=f(x) изображен на рисунке. Укажите наименьшее значение этой функции 1 на отрезке [a;b]. а b 0 1 x 1) 0; 2) -4,5; 3) -2; 4) -3. 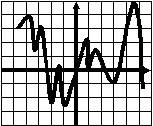2. у На рисунке изображен график функции у=f(x). Сколько точек максимума имеет функция? 1 0 1 х 1) 5; 2) 6; 3) 4; 4) 1. 3. В какой точке функция у= 2х2+24х -25 принимает наименьшее значение? 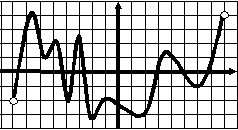1) -4; 2) -2; 3) -6; 4) 6. 4. Функции у=f(x) задана на отрезке [a;b]. у На рисунке изображен график ее производной у=f ´(x). Исследуйте на экстремумы 1 b функцию у=f(x). В ответе укажите количество a 0 1 х точек минимума. 1) 6; 2) 4; 3) 7; 4) 5. 5. Найдите наибольшее значение функции у= -3х2+12х -7. 1) 5; 2) 7; 3) 1; 4) 2. 6. Найдите наибольшее значение функции на отрезке [-3;-1]. 1) -; 2) -5; 3) -1; 4) - 4. 7. Найдите наименьшее значение функции у=|2х-7| + 3. 1) -; 2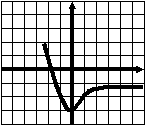) -2 3) 3; 4) -5. 8. При каком значении параметра р функция имеет минимум в точке хо= -2 ? 1) -24; 2) -6; 3) -12; 4) 6. у 9. Укажите наименьшее значение функции у=f(x), график которой изображен на рисунке. 1 х 0 1 1) -1,5; 2) -1; 3) -3; 4) 0. 10. Найдите наибольшее значение функции у=log11 (121 –x2). 1) 11; 2) 121; 3) 1; 4) 2. 11. Найдите наибольшее значение функции у=2cos+3. 1) 5; 2) 3; 3) 2; 4) .