№
|
Задание
|
B1
|
Призерами городской олимпиады по математике стал 31 ученик, что составило 25% от числа участников. Сколько человек участвовало в олимпиаде?
|
B2
|
На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, сколько дней из данного периода среднесуточная температура была от 2 до 7 градусов Цельсия.
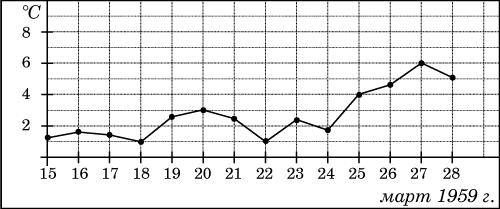
|
B3
|
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
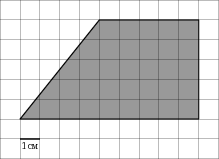
|
B4
|
От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.
Автобусом
|
Электричкой
|
Маршрутным такси
|
От дома до автобусной
станции — 20 мин
|
От дома до станции
железной
дороги — 15 мин
|
От дома до остановки
маршрутного
такси — 15 мин
|
Автобус в пути:
2 ч 10 мин
|
Электричка в пути:
1 ч 30 мин
|
Маршрутное такси
в дороге: 1 ч 5 мин
|
От остановки автобуса
до дачи пешком 5 мин
|
От станции до дачи
пешком 45 мин
|
От остановки маршрутного
такси до дачи
пешком 80 минут
|
|
B5
|
Найдите корень уравнения: 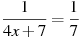
|
B6
|
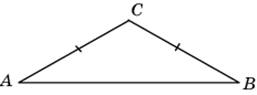
В треугольнике ABC AC = BC, угол C равен 120o, 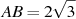 . Найдите AC. . Найдите AC.
|
B7
|
Найдите 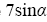 , если , если 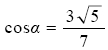 и и 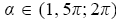
|
B8
|
Прямая y = x является касательной к графику функции ax2 – 23x + 6. Найдите a.
|
B9
|
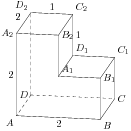
Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
|
B10
|
Научная конференция проводится в 4 дня. Всего запланировано 50 докладов — первые два дня по 11 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
|
B11
|
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
|
B12
|
Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой 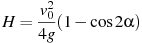 , где v0= 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с2). При каком наименьшем значении угла , где v0= 20 м/с — начальная скорость мячика, а g — ускорение свободного падения (считайте g=10 м/с2). При каком наименьшем значении угла  (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м? (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
|
B13
|
Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
|
B14
|
Найдите наибольшее значение функции 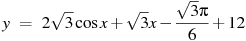 на отрезке на отрезке 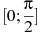
|
 Скачать 35.87 Kb.
Скачать 35.87 Kb.