№
|
Задание
|
B1
|
Мобильный телефон стоил 7500 рублей. Через некоторое время цену на эту модель снизили до 4200 рублей. На сколько процентов была снижена цена?
|
B2
|
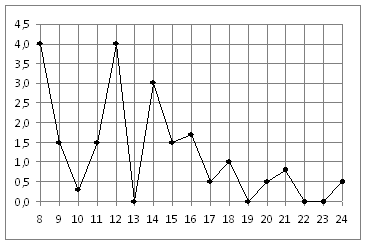
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа за данный период впервые выпало ровно 1,5 миллиметра осадков.
|
B3
|
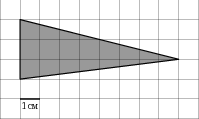
На клетчатой бумаге с клетками размером 1 х 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
|
B4
|
В среднем гражданин А. в дневное время расходует 110 кВт*ч электроэнергии в месяц, а в ночное время — 155 кВт*ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,2 руб. за кВт*ч. Год назад А. установил двухтарифный счeтчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,2 руб. за кВт*ч, а ночной расход оплачивается по тарифу 0,7 руб. за кВт*ч.
В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.
|
B5
|
Найдите корень уравнения 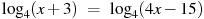
|
B6
|
В тупоугольном треугольнике ABC AC = BC, высота AH равна 2,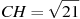 . Найдите sinACB. . Найдите sinACB.
|
B7
|
Найдите значение выражения 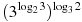
|
B8
|
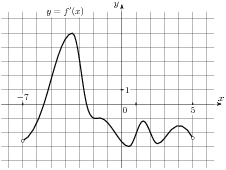
На рисунке изображен график y = f '(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
|
B9
|
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SB=10 , BD=12. Найдите длину отрезка SO.
|
B10
|
В сборнике билетов по математике всего 60 билетов, в 9 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по производной.
|
B11
|
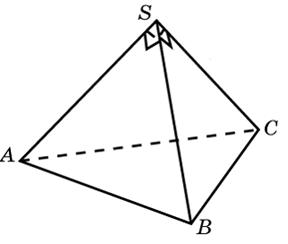
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
|
B12
|
Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 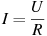 , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах. , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
|
B13
|
Из городов A и B, расстояние между которыми равно 390 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 225 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
|
B14
|
Найдите наименьшее значение функции 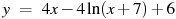 на отрезке на отрезке 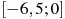
|
 Скачать 29.75 Kb.
Скачать 29.75 Kb.